Counting

Counting is a process used to determine how many of something there is, like how many apples John has, or how many minutes it takes to make a cup of coffee.

Learning to count, like learning to read, walk, or talk, is a common developmental milestone in a child's life in many cultures around the world. It is often a child's first step into mathematics. This page covers some of the different forms or methods of counting as well as some strategies for developing a sense of numbers, quantities, and counting.

Types of counting

There are a number of different methods of counting.

What is skip counting?

Skip counting is a method of counting that involves counting by a specific number (other than 1). For example, skip counting by 2 means counting by every 2nd number. If you are skip counting by 2, starting from 0, you would count as follows: 0, 2, 4, 6, 8, 10, and so on. If you are skip counting by 5, starting from 2, you would count as follows: 2, 7, 12, 17, 22, and so on. Although you can skip count starting from any number, when a child is first learning about skip counting, it is helpful to always start from 0. In this way, skip counting may also be useful in the future as an introduction to multiplication.

Another way to think about skip counting involves addition and subtraction. When using addition, skip counting means adding the number you want to skip count by to itself. For example, skip counting by 3 means that the following number in the sequence is found by adding 3 to the previous number; if we start at 0, skip counting by 3 can be shown as follows: 0, (0 + 3) = 3, (3 + 3) = 6, (6 + 3) = 9, (9 + 3) = 12, and so on. The same follows for subtraction except that each following number in the sequence would be 3 less than the previous number.

One way to visualize skip counting is through use of a number line. The figure below shows skip counting by 2 along a number line:


The first number in the sequence is 0. Adding 2 to that and each subsequent result, the counting sequence proceeds as: 0, 2, 4, 6, 8, 10.

Counting with fingers

Finger counting is a particularly useful tool that can help children improve their counting skills as well as their understanding of number ordering. Research has shown that finger counting (as well as other methods involving manipulative elements) is an important step that helps children progress from more elementary thinking towards more abstract thinking.

There are various systems of finger counting that vary across cultures as well as time. Generally, a single finger represents one unit, but the manner in which the fingers are raised when counting each number varies widely. Below are a few of examples:


The specific system used does not really matter, but developing a link between numbers and fingers that allows children to start to count and have an understanding of "how many" of something there are is important. Whether or not a child uses their fingers to count, or can count mentally, does not necessarily mean that a child has a lesser or greater math capability. When teaching a child to count, focus on their understanding of important counting principles, rather than specifically how they count. If finger counting (or the use of other objects) works for the child, do not discourage it in favor of forcing mental math based on the false premise of mental math inherently indicating higher math capability. Before children can move on to abstract concepts, they must first have a solid grounding to do so.

Tally marks

Counting can also be done through use of tally marks. Tally marks are useful for counting something over a period of time, such as the number of days passed, the number of pieces of candy you eat throughout a day, or the number of points scored at a given point in a game. Tally marks are written as vertical lines, where each line represents 1 unit, and are typically written in groups of 5, where the 5th mark is a diagonal line through the first 4, as shown below:

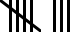
The tally marks above represent the number 8.

Verbal/mental counting

One other form of counting is verbal or mental counting. Verbal or mental counting involves speaking each number out loud (or in your head). This form of counting is more useful when counting things that are present, such as the number of books on a bookshelf, rather than counting things over time.

Counting principles

There are a number of counting principles that can be used to track the progression of a child's understanding of counting. This in turn can give us an idea of what stage the child's development of number sense is in.

Generally, counting can be categorized as rote counting and rational counting. Rote counting is the type of counting we all begin with, which involves memorizing the names of numbers in the correct order. For example, if a child can count "one, two, three, four, five," the child has mastered rote counting up to the number 5. This form of counting, while necessary, is limited, since all it shows is the ability to memorize and count up to (or by) a certain number; it does not display any understanding of what those numbers mean or an ability to use them in a meaningful way.

On the other hand, rational counting is achieved when there is an understanding of the numbers being counted. For example, given that there are 3 pieces of chocolate, if a child can count each piece of chocolate and conclude that there are 3 pieces of chocolate, this is evidence of rational counting. More specifically, rational counting displays an understanding that there are principles that apply to any set of objects being counted that allow us to determine how many objects there are in a set. This concept of "how many" is another important aspect of rational counting.

Four basic counting principles that indicate rational counting are stable order, one-to-one correspondence, order irrelevance, and cardinality, each of which builds upon the previous principle.

Stable order

The stable order principle states that each number needs to be named in the same order every time when counting. For example, "one, two, three, four, five." If numbers are not counted in this way, it does not constitute counting or an understanding of the stable order principle. For example, if a child counts "one, three, seven, twenty-two," and so on, the child may know the number names, but may not have a strong grasp of the stable order principle.

The stable order principle involves understanding the concept that each number (when counting) is always one more than the previous number in the count, and one less than the following number. For example, the number 7 is one more than 6, and one less than 8. It follows that 8 is larger than 7, which is in turn larger than 6. This relationship is one of the starting points of developing number sense and an understanding of mathematical structure that is missing in rote counting.

One-to-one correspondence

The one-to-one correspondence principle states that when counting objects, each object is named by only one number. For example, if there are 3 cookies, each cookie can only be named by the number 1, 2, or 3. While this is a relatively straightforward concept, it can take time for a child to develop this understanding.

One way to help develop a child's understanding of this principle is to provide a set of objects that they can tag as they count, matching one number to one object until they have tagged each object. Common mistakes include a child tagging each object correctly, but using the wrong number words; tagging objects more than once; or missing objects when tagging. In the first case, the child may understand the one-to-one correspondence principle, but may need more practice with rote counting. In the second two cases, the child is still missing the understanding that each object must have a corresponding number word, which may be helped with more intentionally tagging the objects. For example, having the child move each object to a different pile once counted may help them to better understand the one-to-one correspondence principle.

Order irrelevance

The order irrelevance principle builds on both the stable order and one-to-one correspondence principles and states that no matter the order in which a collection of objects is counted, the result is the same. Given 5 different objects, no matter how they are placed or counted, be it from left to right, right to left, and so on, the count will always be 5. One simple way to demonstrate this principle, as well as the fact that an "object" being counted can be anything including things that are more abstract, is to have children count their classmates. For example, Ana, Joe, Bailey, Chloe, and Kyle are 5 students in a class. No matter who Ana counts first or last, counting each of her classmates will result in a count of 4. Also, it is important to understand that each number word is applied only temporarily to a given object when counting. Using the same example, Ana may count Joe as "one," Chloe as "two," Kyle as "three," and Bailey as "four." She could also count Bailey as "one," Chloe as "two," Joe as "three," and Kyle as "four." Helping children practice counting the same objects in different ways while arriving at the same total number can help them understand the order irrelevance principle, which in turn helps them develop more flexible thinking when they start to realize that there are many different methods and strategies for counting the same objects.

Cardinality

The principle of cardinality builds on all the previously mentioned principles: objects being counted each have a single number applied to them in the correct sequence (stable order principle) and are counted only once (one-to-one correspondence). The order in which the objects are counted does not impact the final count (order irrelevance), and the final count of the set of objects after applying all of these principles is its cardinality. For example, after counting 17 objects, we can conclude that the cardinality of the set is 17.

After correctly counting a set of objects, a child who understands cardinality should be able to respond to the question "how many objects are there" by replying with the final number counted. A child who must count the objects again to respond might not fully understand cardinality. Furthermore, a child who understands cardinality should be able to count out a specified number of objects. For example, given 20 oranges, the child should be able to count out 5 oranges from the set if asked. Also, if the 5 oranges are then rearranged and the child is asked how many oranges there are, a response that shows the child understands that there are still 5 oranges, despite the rearrangement, would indicate an understanding of cardinality.