Convergent sequence

Convergence is a concept used throughout calculus in the context of limits, sequences, and series. A convergent sequence is one in which the sequence approaches a finite, specific value. Consider the sequence . We can determine whether the sequence converges using limits. A sequence converges if its nth term, an, is a real number L such that:



Referencing the above example,


 
 

Since ,



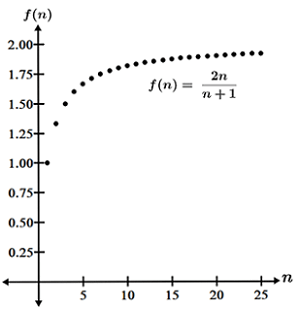
Thus, the sequence converges to 2. The figure below shows the graph of the first 25 terms of the sequence, which demonstrates the trend of the sequence towards 2 (though alone it would not be sufficient to conclude that the sequence converges to 2).



Techniques for determining convergence

A sequence converges if the limit of its nth term exists and is finite. Thus, the various methods used to find limits can also be applied when trying to determine whether a sequence converges.

Comparing degrees of rational functions

If an is a rational expression of the form , where P(n) and Q(n) represent polynomial expressions, and Q(n) ≠ 0, first determine the degree of P(n) and Q(n). Then:

Example

Determine whether the following sequence converges:

The degree of P is 2 and the degree of Q is 2. Since the degree of P and Q are equal, the sequence converges, and the limit is the ratio of the coefficients of their respective n2 terms:



Using L'Hôpital's rule

In some cases, it is possible to use L'Hôpital's rule to determine whether a sequence converges.

Use L'Hôpital's rule to determine whether the following sequence converges:

The limit of the sequence results in an indeterminate form ∞/∞, so apply L'Hôpital's rule:



The above limit still results in an indeterminate form ∞/∞, so apply L'Hôpital's rule again:



Since the limit exists and is finite, the sequence converges.

Convergence of geometric sequences

A geometric sequence is a sequence in which each successive term after the first is determined by multiplying the previous term by a fixed number referred to as the common ratio. The nth term of a geometric sequence is



where r is the common ratio, and can be determined as for n = 1, 2, 3,... n. A geometric sequence converges if -1 < r ≤ 1 and diverges if r ≤ -1 or r > 1. If r = 1, the geometric sequence will be a sequence of identical constants, and is therefore trivial.


Examples

Determine whether the following geometric sequences converge:



i. To determine whether a geometric sequence converges, first find r. We will do so using a1 and a2:


 
 
 
 

Since -1 < ½ ≤ 1, the sequence converges.


ii. Find r using a1 and a2:


 

Since -2 ≤ -1, the sequence diverges.


iii. The sequence can be simplified by multiplying the bases and raising them to the same exponent:



Then, to determine whether the sequence converges, find r using a1 and a2:


 

Since -1 < -½ ≤ 1, the sequence converges.

Bounded monotonic sequences

If a sequence is both bounded and monotonic, the sequence converges. A bounded sequence is one in which there exist real numbers, A and B, for n = 1, 2, 3, ..., such that A ≤ an ≤ B. A sequence is monotonic if it is only increasing or decreasing. In other words, a1 ≤ a2 ≤ a3 ≤ ... ≤ an or a1 ≥ a2 ≥ a3 ≥ ... ≥ an.

Referencing the sequence in example i from the previous section, , we can determine the first terms:



As can be seen, the sequence is decreasing, and since each successive term is determined by multiplying the previous term by ½, we know that the sequence will continue to decrease (and never increase), and is therefore monotonic. The upper bound of the sequence is therefore 4, and the lower bound can be found by determining the limit of the nth term:



Thus, the lower bound is 0, and since the sequence is both monotonic and has an upper bound and lower bound, it converges.