ln
The natural logarithm is a logarithm in which the base is the mathematical constant, e. It is written as ln(x) or loge(x). In certain contexts, log(x) is also used to refer to the natural log. However, log(x) is more commonly used to refer to log10(x). Using ln(x) or loge(x) to refer to the natural log removes this ambiguity.
The natural log is used widely throughout mathematics and physics. Logarithms in general are particularly useful for solving equations that involve variables in the exponent, since a logarithm can be applied to both sides of the equation to "bring the exponent down."
Example
Find x for ex = 12.
ex = 12
ln(ex) = ln(12)
x = ln(12)
This works because ln(x) is the inverse function of the exponential function, ex. In other words:
eln(x) = x, if x > 0
ln(ex) = x
Natural logarithm function
The natural logarithm can be defined as the area under the curve of the graph y = . For a given real number, a, the natural logarithm is the area between x = 1 and x = a. This can be more clearly defined using calculus:
Below is a graph of the natural logarithm function.
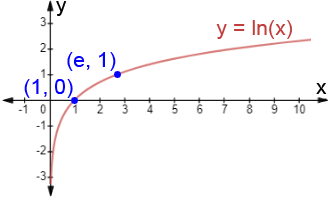
Like the graph of the logarithm of any other base, the natural logarithm function has an x-intercept, or zero/root at x = 1, as shown by the point (1, 0) in green. At x = e), the function has a value of 1. In other words:
ln(e) = 1
ln(1) = 1
As x approaches 0, ln(x) approaches -∞. As x approaches ∞, ln(x) approaches ∞.
Natural logarithm rules/properties
Natural logarithms share the same basic logarithm rules as logarithms with other bases.
- Product rule: ln(mn) = ln(m) + ln(n), for x > 0 and y > 0
- Quotient rule: ln(
) = ln(m) - ln(n)
- Power rule: ln(mn) = n·ln(m), for x > 0
Another useful property of logarithms is that they can be expressed in terms of logarithms of other bases multiplied by a constant. For example, to convert between a base 10 logarithm and the natural logarithm, use the following formulas:
Example
Convert the following logarithms between base 10 and base e.
1. ln(2):
2. log10(e):
