Discriminant
The discriminant describes a characteristic of the roots of polynomials. It discriminates different polynomials of the same type from each other.
There are different discriminants used for different degrees of polynomials, but the one you're most likely to see, especially in algebra, is b2 - 4ac, which is used to describe the number of solutions a quadratic has. Although this is only one discriminant, the term "discriminant" is often used to refer to this specific discriminant. This discriminant is also used as part of the quadratic formula within the radical in the numerator.
If the discriminant is less than 0, then the quadratic has no real solution. You can remember this by recalling that you cannot take the square root of a negative number (without using imaginary numbers). In the quadratic formula, the discriminant is enclosed within a radical, so if the discriminant is negative, then you will not be able to calculate a real solution.
Example
f(x) = 3x2 - 2x + 2
a = 3 ; b = -2 ; c = 2
b2 - 4ac = (-2)2 - 4(3)(2)
= 4 - 24 = -20
If the discriminant is negative, there is no real solution. As can be seen in the figure below, there are no zeros on the graph:
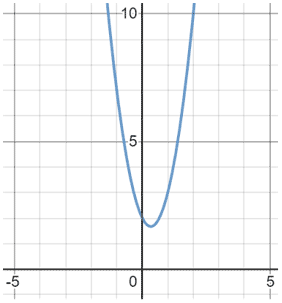
If the discriminant is equal to 0, then the quadratic has one solution. You can remember this by recalling that the square root of 0 is 0. Below is an example of this case:
Example
| f(x) = 4x2 - 4x + 1 |
| a = 4 ; b = -4 ; c = 1 |
| b2 - 4ac = (-4)2 - 4(4)(1) |
| = 16 - 16 = 0 |
| f(x) = 4x2 - 4x + 1 |
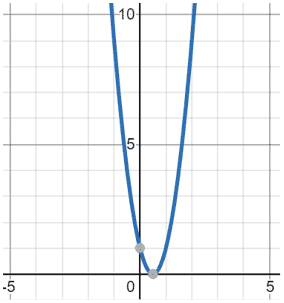
The discriminant is 0 and there is one solution at x = ½
If the discriminant is greater than 0, then the quadratic has two solutions. You can remember this by recalling that the square root of a positive number has two solutions, one positive and one negative, as shown below:
Example
| f(x) = x2 - 2x - 3 |
| a = 1 ; b = -2 ; c = -3 |
| b2 - 4ac = (-2)2 - 4(1)(-3) |
| = 4 + 12 = 16 |
Since the discriminant is greater than 0, two solutions exist: x = -1 or x = 3.
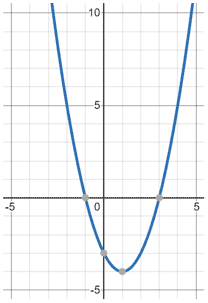
See also quadratic formula.
