System of equations
Systems of equations are sets of equations where the solution is the intersecting point(s) between the equations. Most of the systems of equations you see in algebra are sets of two linear equations in the standard form Ax + By = C.
There are three methods typically used to solve systems of linear equations: graphing, the substitution method, and the elimination method. These methods can be applied to more complex systems of nonlinear equations as well.
Graphing method
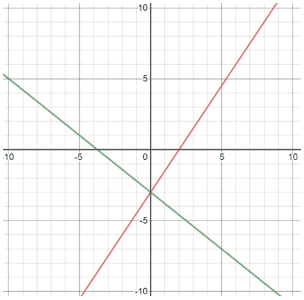
Solving systems of equations by graphing is done by graphing each equation in the system and identifying the point(s) of intersection. It may be easier to graph the equations by converting the standard form of each equation to slope-intercept form.
Example
|
|
Substitution method
Solving systems of equations using the substitution method involves replacing a variable in one equation with the equivalent of that variable, calculated using the other equation. Refer below for an example.
The first step of the substitution method is to solve for a variable in one equation.
You can decide which variable to solve for by examining each coefficient. Variables with coefficients of 1 are the easiest to solve for because you will not have to divide by anything. Variables with coefficients that do not divide well into other coefficients create messy fractions.
Example
| 3x + y = 31 | → | y = -3x + 31 |
| 2x - 5y = 15 | → | -5y = 15 - 2x |
Next, substitute the equivalent of the variable you just solved for into the corresponding variable in the other equation.
y = -3x + 31
2x - 5y = 15
2x - 5(-3x + 31) = 15
Now, because there is only one variable left in the equation, you can solve for that variable!
2x - 5 (-3x + 31) = 15
2x + 15x - 155 = 15
17x = 170
x = 10
To solve for the remaining variable, you can plug in the value of the variable you just solved for into either of the original equations.
x = 10
2(10) - 5y = 15
-5y = -5
y = 1
Now you have the values of both coordinates! The solution to the system of equations is (10, 1).
You can check your answers by plugging the x- and y-values into the original equations and simplifying. If both equations return true statements, as shown below, then you have successfully used the subtitution method!
| x = 10 | y = 1 |
| 3x + y = 31 | 2x - 5y = 15 |
| 3(10) + (1) = 31 | 2(10) - 5(1) = 15 |
| 31 = 31 | 15 = 15 |
Elimination method
To solve systems of equations using the elimination method, you need to eliminate one variable. Before starting, it is very important that both equations are in the standard form Ax + By = C. This organizes the systems of equations by aligning each term in one equation with their corresponding term in the other.
When using the elimination method, try to think of the system of equations as one big addition column, except that there is no carrying, and you can only add and subtract corresponding variables and constants.
Example
| 6x + 2y | = 18 | |
| + | 5x + 4y | = 22 |
| ? |
The goal of elimination is to cancel out a variable. This means that when you have the equations lined up by column and variable, as in the example above, you want the sum of the column of a variable to equal 0. To accomplish this, you need to multiply one, or sometimes both, of the equations in the system by a constant that will create a coefficient that is of equal value, but opposite sign from the corresponding variable in the other equation.
To decide which equation to use and what constant to multiply it by, we can examine each pair of variables. Ask yourself: "What can I multiply this variable by to cancel out the variable in the other equation?"
In the example, 6x and 5x are more difficult to manipulate to cancel out than 2y and 4y. You could multiply the top equation by (or the bottom one by
but this would make the rest of either equation more difficult to work with. You could also multiply the top equation by 5 and the bottom one by -6, but this also produces numbers that are more difficult to work with than the option presented below.
Using 2y and 4y results in a relatively easy equation to work with, since you can multiply the first equation by -2 to cancel out the 4y in the second equation, as shown below.
| -2(6x + 2y | = | 18) | |
| + | 5x + 4y | = | 22 |
| ? |
| -12x - 4y | = | -36 | |
| + | 5x + 4y | = | 22 |
| ? |
Note: Don't forget to multiply the entire equation by the constant, including the right side of the equals sign. If you don't multiply the entire equation, it will not be the same equation anymore!
Now you can add each column:
| -12x - 4y | = | -36 | |
| + | 5x + 4y | = | 22 |
| -7x + 0 | = | -14 |
Then solve for x!
| -7x | = -14 |
| x | = 2 |
Next, plug the value of x into one of the original equations to find the value of y.
| x | = 2 |
| 5(2) + 4y | = 22 |
| 4y | = 12 |
| y | = 3 |
Now you have the values of both coordinates. Thus, the solution to the system of equations is (2, 3).
You can then check if your solution is correct by plugging the x and y-values into the original equations.
| x = 2 | y = 3 |
| 6x + 2y = 18 | 5x + 4y = 22 |
| 6(2) + 2(3) = 18 | 5(2) + 4(3) = 22 |
| 12 + 6 = 18 | 10 + 12 = 22 |
| 18 = 18 | 22 = 22 |
Systems of linear equations will have no solution (parallel lines), one solution (intersecting lines), or infinite solutions (identical lines).
The examples above all had one solution. Let's examine the other cases.
When a system of linear equations has no solution, the lines are parallel to each other and will therefore never intersect.
Every method you try will result in the elimination of both variables and simplifying it will leave you with a statement that is not true.
Example
| -15x + 3y | = 9 |
| -5x + y | = 2 |
First using the substitution method:
| y = 5x + 2 |
| -15x + 3(5x + 2) | = 9 |
| -15x + 15x + 6 | = 9 |
| 6 = 9 |
The result obtained through the substitution method yields a false statement since 6 ≠ 9.
Using the elimination method:
| -15x + 3y | = 9 | |
| + | (-3)(-5x + y | = 2) |
| ? |
| -15x + 3y | = 9 | |
| + | 15x - 3y | = 6 |
| 0 + 0 | ≠ | 3 |
The result obtained through the elimination method also yields a false statement since 0 ≠ 3
Using the graphing method:
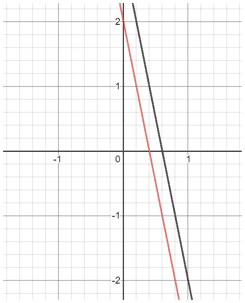
Since the lines are parallel, they have the same slope, and will never intersect. Therefore, there is no solution to the system of equations.
Using this knowledge, it is possible to recognize systems of linear equations in which there is no solution because the coefficients of each set of variables will be multiples of each other, and both pairs will have the same multiplier (the number you multiply to get the multiple). If the constants are not multiples, or do not have the same multiplier as the coefficients, then the system will have no solution.
On the other hand, if you can multiply one of the equations in the system by a constant to obtain exactly the other equation, it means that the equations describe the same line, and that the system will have infinite solutions. Systems of linear equations with infinite solutions will cancel out both variables, yielding a true statement. This is because identical lines have the same slope and y-intercept and will intersect at every point.
Example
| -15x + 3y | = 9 |
| -5x + y | = 3 |
Substitution method:
| y = 5x + 3 |
| -15x + 3(5x + 3) | = 9 |
| -15x + 15x + 9 | = 9 |
| 9 = 9 |
Since the result of using the substitution method is a true statement, 9 = 9, the system of equations has infinite solutions.
Elimination method:
| -15x + 3y | = 9 | |
| + | (-3)(-5x + y | = 3) |
| ? |
| -15x + 3y | = 9 | |
| + | 15x - 3y | = -9 |
| 0 + 0 | = | 0 |
Like the substitution method, since the result of the elimination method is another true statement, 0 = 0, the system of equations has infinite solutions.
Graphing method:
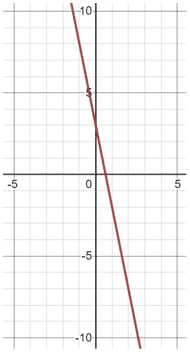
The graph of the two equations allows us to see what looks like only one line. This is because the system of equations defines the same line, confirming that there are infinite solutions.