Exponential function
An exponential function is a function that grows or decays at a rate that is proportional to its current value. It takes the form:
f(x) = abx
where a is a constant, b is a positive real number that is not equal to 1, and x is the argument of the function. A defining characteristic of an exponential function is that the argument (variable), x, is in the exponent of the function; 2x and x2 are very different. 2x is an exponential function, while x2 is not:
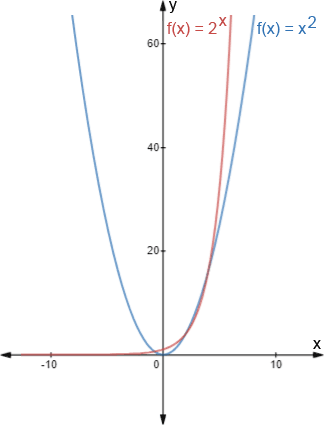
The figure above shows the graphs of 2x (red) and x2 (blue). The graph in red is representative of exponential functions; exponential functions don't have y-values below 0. At large negative x-values, exponential functions approach 0, and stay very small up until they start increasing. Once an exponential function begins increasing, its rate of increase grows rapidly, and the graph quickly approaches positive infinity.
To really demonstrate how fast an exponential function increases, plot some values for the function f(x) = x2 and f(x) = 2x:
| x | f(x)=x2 | f(x)=2x |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 4 | 4 |
| 3 | 9 | 8 |
| 10 | 100 | 1024 |
| 20 | 400 | 1,048,577 |
| 30 | 900 | 1,073,741,824 |
If the argument is further scaled by a positive number greater than 1 (eg. 25x), the exponential function will increase even more quickly.
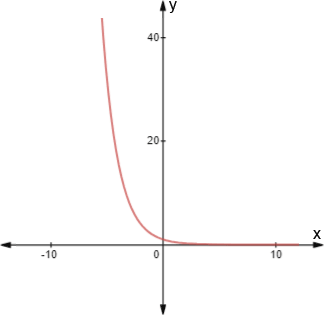
A negative argument results in exponential decay, rather than exponential growth. This means that the graph rapidly decreases towards 0 as x increases. Below is a graph of f(x) = 2-x.
For values of the base between 0 and 1, such as f(x) = 0.3x, the graph of the exponential function also approaches 0 as x approaches infinity.
