Exponential
In algebra, the term "exponential" usually refers to an exponential function. It may also be used to refer to a function that exhibits exponential growth or exponential decay, among other things.
Exponential function
An exponential function is a function that grows or decays at a rate that is proportional to its current value. It takes the form of
f(x) = bx
where b is a value greater than 0. The rate of growth of an exponential function is directly proportional to the value of the function. There are a few different cases of the exponential function.
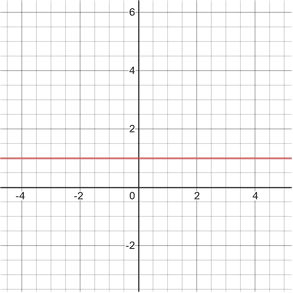
when b = 1
When b = 1 the graph of the function f(x) = 1x is just a horizontal line at y = 1. This is because 1 raised to any power is still equal to 1.
when b > 1
For f(x) = bx, when b > 1, the graph of the exponential function increases rapidly towards infinity for positive x values. For negative x values, the graph of f(x) approaches 0, but never reaches 0. There is a horizontal asymptote at y = 0, meaning that the graph never touches or crosses the x-axis. Below is the graph of the exponential function f(x) = 3x.
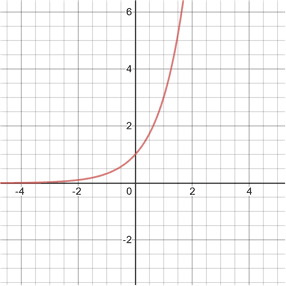
The graph above demonstrates the characteristics of an exponential function; an exponential function always crosses the y axis at (0, 1), and passes through a (in this case 3), at x = 1. The key characteristic of an exponential function is how rapidly it grows (or decays). Just as an example, the table below compares the growth of a linear function to that of an exponential one.
| x = 1 | x = 2 | x = 3 | x = 4 | x = 5 | |
|---|---|---|---|---|---|
| 3x | y = 3 | y = 9 | y = 27 | y = 81 | y = 243 |
| 3x | y = 3 | y = 6 | y = 9 | y = 12 | y = 15 |
In the table above, we can see that while the y value for x = 1 in the functions 3x (linear) and 3x (exponential) are both equal to 3, by x = 5, the y value for the exponential function is already 243, while that for the linear function is only 15.
when 0 < b < 1
When b is between 0 and 1, rather than increasing exponentially as x approaches infinity, the graph increases exponentially as x approaches negative infinity, and approaches 0 as x approaches infinity. Below is the graph of .
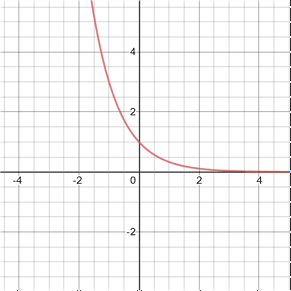
The graph of the exponential function for values of b between 0 and 1 shares the same characteristics as exponential functions where b > 0 in that the function is always greater than 0, crosses the y axis at (0, 1), and is equal to b at x = 1 (in the graph above (1, ⅓)). Compared to the shape of the graph for b values > 1, the shape of the graph above is a reflection across the y-axis, making it a decreasing function as x approaches infinity rather than an increasing one.
Natural exponential function
The natural exponential function is f(x) = ex. Since any exponential function can be written in the form of ex such that
bx = ex ln(b)
ex is sometimes simply referred to as the exponential function. It can also be denoted as f(x) = exp(x). As an example, exp(2) = e2. Like the exponential functions shown above for positive b values, ex increases rapidly as x increases, crosses the y-axis at (0, 1), never crosses the x-axis, and approaches 0 as x approaches negative infinity.
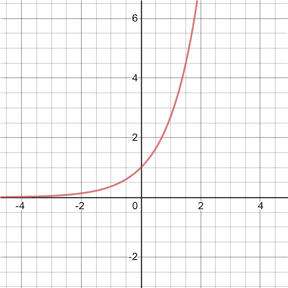
One important property of the natural exponential function is that the slope the line tangent to the graph of ex at any given point is equal to its value at that point. In other words, the rate of change of the graph of ex is equal to the value of the graph at that point.
Example
For f(x) = ex, and slope m:
f(0) = e0 = 1 = m
f(1) = e1 = e = m
f(½) = e½ = 1.649 = m
In calculus, this is apparent when taking the derivative of ex. Functions of the form f(x) = aex, where a is a real number, are the only functions where the derivative of the function is equal to the original function.
The area under the curve (also a topic encountered in calculus) of ex is also equal to the value of ex at x.
