Fourier series
A Fourier series is a way to represent a periodic function in terms an infinite sum of sines and cosines. Fourier series are useful for breaking up arbitrary periodic functions into simpler terms that can be individually solved, then recombined to provide a solution or approximation to a given problem. For this reason, Fourier series can be used to solve a wide variety of mathematical problems within fields such as acoustics, engineering, signal processing, econometrics, and more.
Fourier series definition
There are a few different forms for representing a Fourier series. This page will be focused on the amplitude-phase form.The Fourier series for a function, y = f(x), with a period of 2L in amplitude-phase form is,
where a0, an, and bn are:
As an example, let's generate the Fourier series for the function f(x) = x from [-π, π], where f(2π + x) = f(x). In other words, the period is 2π, so L = π. Then,
Thus, a0 = 0, and we compute an next:
The definite integral can be computed using integration by parts. Let dv = cos(nx)dx and u = x, then and du = dx. Substituting these values into,
,
Thus, an = 0, and finally we compute bn:
The definite integral can again be computed using integration by parts. Let dv = sin(nx)dx and u = x, then and du = dx. Substituting into the integration by parts formula:
Since for all values of n,
, and:
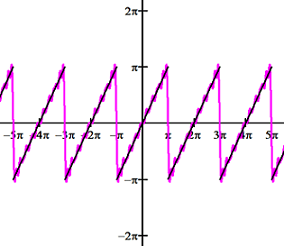
Below is the graph of the Fourier series, where the purple represents the Fourier series superimposed on top of the periodic extension of the function y = x. It is referred to as a saw-tooth wave due to its shape emulating the teeth of a saw.
Fourier series for even/odd functions
Note that in the example above, because f(x) is an odd function, an = 0, and the Fourier series does not have a cosine term, so the Fourier series collapses to,
where
This is referred to as the Fourier sine series. Similarly, if f(x) is an even function, then bn = 0, and there is no sine term, so the Fourier series collapses to:
where
and
This is referred to as the Fourier cosine series. As an example, let's generate the Fourier cosine series for f(x) = x2, an even function, over the interval [-π, π]:
and
The definite integral can be calculated using integration by parts, where dv = cos(nx)dx, u = x2, , and du = 2xdx. Substituting these into the integration by parts formula:
The definite integral can be calculated using integration by parts, where dv = sin(nx)dx, u = x, , and du = xdx. Substituting these into the integration by parts formula:
Since cos(πn) = (-1)n for all values of n,
,
and the Fourier cosine series is:
Fourier series over any interval
In the examples above, the functions had periods of 2π, which made finding the coefficients more convenient since the integrals involved sines and cosines. However, it is also possible to find the Fourier series of a function in a similar manner even if the period is not 2π. Consider the function f(x) = x (an odd function) over the interval [-2, 2], where f(4 + x) = f(x). Since the period is 4 units, L = 2, and a0 and an can be computed as follows:
The definite integral can be computed using integration by parts, where , u = x,
, and du = dx. Substituting these into the formula for integration by parts:
Thus, an = 0. Recall that since the function is odd over the given interval, a0 and an will always be zero, as shown above, so it is only necessary to compute bn:
The definite integral can be computed using integration by parts, where , u = x,
, and du = dx. Substituting these into the integration by parts formula:
Since for all n,
, and the Fourier series is:
