Taylor series
A Taylor series of a function is a special type of power series whose coefficients involve derivatives of the function. Taylor series are generally used to approximate a function, f, with a power series whose derivatives match those of f at a certain point x = c, called the center. This is because power series are relatively easy to calculate, differentiate, and integrate. With Taylor series, we can approximate values like e1.23 and cos(0.77), or integrate functions like , which we cannot calculate exactly.
The Taylor series for f(x) centered at c is given by:
| f(x) | = | ||
| = |
where f(n)(c) denotes the nth derivative of f at c. The 0th derivative of f at c is just the value f(c). Also remember that 0! = 1, not 0, so
When c = 0, the resulting Taylor series is referred to as the Maclaurin series for f:
| f(x) | = | ||
Example
Generate the first four terms and general term of the Taylor series for e2x centered at x = 1.
Since c = 1,
To generate the first four terms in the series, find the first three derivatives for e2x.
Thus, the nth derivative follows the pattern . Substituting these values into the expanded form of the Taylor series,
The graphs of e2x and its Taylor series containing the first four terms are shown below:
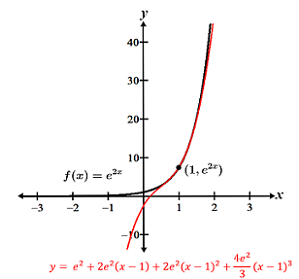
In some cases, the Taylor series representation of a function can only be evaluated within some interval containing the center of the series. This interval is referred to as the interval of convergence for the Taylor series.
Interval of convergence for a Taylor series
For a Taylor series centered at c, the interval of convergence is the interval that contains values of x for which the series converges. In some cases, the interval of convergence is infinite, while in others, only a small range of x values comprise the interval. The center of a Taylor series is also the center of the interval. If there is some positive real number R (the radius of convergence) such that |x = c| < R, the series will converge; if |x - c| > R, the series will diverge.
Solving the inequality |x - c| < R yields:
Thus, the interval of convergence can be written as (c - R, c + R) such that if x lies between these two values, the Taylor series will converge.
To find the radius of convergence (and thus the interval of convergence), the ratio test can be used. The ratio test states that a series will converge if the ratio of its (n + 1)th term to its nth term is less than 1:
As an example, we will use the ratio test to find the interval of convergence for the following Taylor series,
Given the above Taylor series, an and an+1 are,
and applying the ratio test yields:
Thus, the radius of convergence is 3, and solving for x yields:
These are the endpoints of the interval of convergence, both of which need to be tested individually for convergence. Substituting x = 2 into the series yields:
is a divergent p-series (also called the harmonic series), so 2 is not included in the interval of convergence. Substituting x = 8 into the series yields,
which is a convergent alternating series, so 8 is included in the interval of convergence, making the interval of convergence (2, 8].
Using an elementary series to write a Taylor series
Below is a table of Taylor series expansions for a few common functions:
| Function | Taylor series |
|---|---|
n = 1,2,3,... |
|
The above expansions can be used to write a Taylor series for a function that is a composite of one of the functions in the table. For example, we can write the Maclaurin series for the composite function cos(x2) by replacing the x in the power series for cos(x) with x2:
Using a Taylor series to approximate a definite integral
Taylor series can also be useful for evaluating functions that are difficult, if not impossible, to integrate symbolically. For example, we can use the first four terms of the Maclaurin series for ex2 to approximate its definite integral over a given interval. The Maclaurin series for ex2 can be written by replacing x in the power series representation of ex with x2:
Using the first four terms, the definite integral of ex2 from x = 0 to x = 1 can be estimated as follows:
