Concavity
The concavity of the graph of a function refers to the curvature of the graph over an interval; this curvature is described as being concave up or concave down. Generally, a concave up curve has a shape resembling "∪" and a concave down curve has a shape resembling "∩" as shown in the figure below.
| Concave up | Concave down |
|---|---|

|

|
How to find the concavity of a function
There are a number of ways to determine the concavity of a function. If given a graph of f(x) or f'(x), determining concavity is relatively simple. Otherwise, the most reliable way to determine concavity is to use the second derivative of the function; the steps for doing so as well as an example are located at the bottom of the page.
How to find concavity from the first derivative
The first derivative of a function, f'(x), is the rate of change of the function f(x). It can provide information about the function, such as whether it is increasing, decreasing, or not changing. To some degree, the first derivative can be used to determine the concavity of f(x) based on the following:
- If f'(x) is increasing over an interval, then the graph of f(x) is concave up over the interval.
- If f'(x) is decreasing over an interval, then the graph of f(x) is concave down over the interval.
Given a graph of f(x) or f'(x), as well as the facts above, it is relatively simple to determine the concavity of a function.
How to find concavity from the graph of f(x)
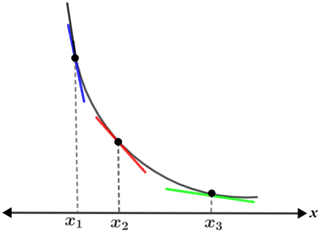
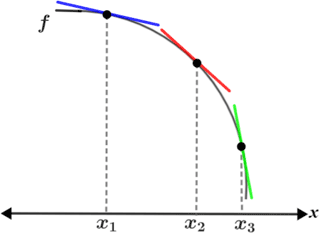
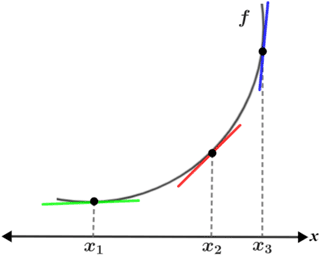
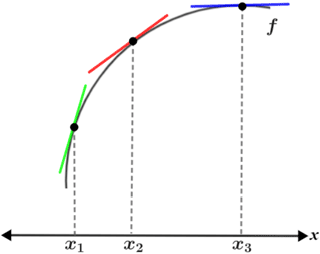
The table below shows various graphs of f(x) and tangent lines at points x1, x2, and x3. Since f'(x) is the slope of the line tangent to f(x) at point x, the concavity of f(x) can be determined based on whether or not the slopes of the tangent lines are decreasing or increasing over the interval.
| Concave up | Concave down |
|---|---|
|
|
| f'(x) is increasing; f(x) is decreasing | f'(x) is decreasing; f(x) is decreasing |
|
|
| f'(x) is increasing; f(x) is increasing | f'(x) is decreasing; f(x) is increasing |
It is important to note that whether f(x) is increasing or decreasing has no bearing on its concavity; regardless of whether f(x) is increasing or decreasing, it can be concave up or down. For example, referencing the figure above, f(x) is decreasing in the first concave up graph (top left panel) and it is increasing in the second (bottom left panel). In both cases, f(x) is concave up. Similarly, in the first concave down graph (top right), f(x) is decreasing, and in the second (bottom right) it is increasing. The change (increasing or decreasing) in f'(x) not f(x) determines the concavity of f(x).
Another way to determine concavity graphically given f(x) (as in the figure above) is to note the position of the tangent lines relative to the graph. When the graph of f(x) is concave up, the tangent lines lie "below" the graph of f(x), and when f(x) is concave down, the tangent lines lie "above."
How to find concavity from the first derivative graph
To determine concavity using a graph of f'(x) (the first derivative), find the intervals over which the graph is decreasing or increasing (from left to right). A graph is increasing or decreasing given the following:
- Given any x1 or x2 on an interval such that x1 < x2, if f(x1) < f(x2), then f(x) is increasing over the interval.
- Given any x1 or x2 on an interval such that x1 < x2, if f(x1) > f(x2), then f(x) is decreasing over the interval.
In the graph of f'(x) below, the graph is decreasing from (-∞, 1) and increasing from (1, ∞), so f(x) is concave down from (-∞, 1) and concave up from (1, ∞). It is neither concave up nor down at x = 1 because f'(x) is not changing.
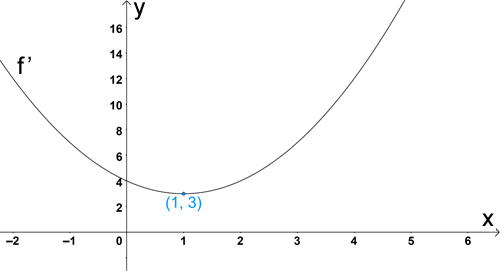
It is important to note that the concavity of f'(x) cannot be used to determine the concavity of f(x); just because f'(x) is concave up does not mean that f(x) is concave up. The graph of f'(x) can only be used to determine the concavity of f(x) based on whether f'(x) is increasing or decreasing over a given interval.
Also, it can be difficult, if not impossible, to determine the interval(s) over which f'(x) is increasing or decreasing without a graph of the function, since every x-value on a given interval would need to be checked to confirm that f'(x) is only increasing or decreasing (and not changing directions) over that interval. Fortunately, the second derivative can be used to determine the concavity of a function without a graph or the need to check every single x-value. It is for this reason that given some function f(x), assuming there are no graphs of f(x) or f'(x) available, the most effective way to determine the concavity of f(x) is to use its second derivative.
How to find concavity from the second derivative
To use the second derivative to find the concavity of a function, we first need to understand the relationships between the function f(x), the first derivative f'(x), and the second derivative f"(x). The derivative of a function represents the rate of change, or slope, of the function. The same way that f'(x) represents the rate of change of f(x), f"(x) represents the rate of change, or slope, of f'(x).
Because a function is increasing when its slope is positive, decreasing when its slope is negative, and not changing when its slope is 0 or undefined, the fact that f"(x) represents the slope of f'(x) allows us to determine the interval(s) over which f'(x) is increasing or decreasing, which in turn allows us to determine where f(x) is concave up/down:
- If f"(x) > 0 for all x on an interval, f'(x) is increasing, and f(x) is concave up over the interval.
- If f"(x) < 0 for all x on an interval, f'(x) is decreasing, and f(x) is concave down over the interval.
- If f"(x) = 0 or undefined, f'(x) is not changing, and f(x) is neither concave up nor concave down. At these points, the sign of f"(x) may change from negative to positive or vice versa; if it changes, the point is an inflection point and the concavity of f(x) changes; if it does not change, then the concavity stays the same.
Given these facts, we can now put everything together and use the second derivative of a function to find its concavity.
Steps for finding concavity
The following steps can be used as a guideline to determine the interval(s) over which a function is concave up or concave down:
- Compute the second derivative of the function.
- Set the second derivative of the function equal to 0 and solve for x.
- Use the x-value(s) from step two to divide the interval into subintervals; each of these x-value(s) is a potential inflection point.
- Test values within each subinterval to determine whether the function is concave up (f"(x) > 0) or concave down (f"(x) < 0) in each subinterval.
Because the sign of f"(x) can only change at points where f"(x) = 0 or undefined, only one x-value needs to be tested in each subinterval since the sign of f"(x) will be the same for each x-value in a given subinterval.
Determine the concavity of:
1. Find f"(x):
2. Solve for f"(x) = 0:
3. Determine the relevant subintervals:
Since f"(x) = 0 at x = 0 and x = 2, there are three subintervals that need to be checked for concavity: (-∞, 0), (0, 2), and (2, ∞).
4. Test values within each interval:
| Subinterval | Sign of f"(x) at test value | Concavity |
|---|---|---|
| (-∞, 0) | (+) ; f"(-1) = 9 | Concave up |
| (0, 2) | (-) ; f"(1) = -3 | Concave down |
| (2, ∞) | (+) ; f"(3) = 9 | Concave up |
