Inflection point
An inflection point is a point where the graph of a function changes concavity from concave up to concave down, or vice versa. Since concavity is based on the slope of the graph, another way to define an inflection point is the point at which the slope of the function changes sign from positive to negative, or vice versa:

Before the inflection point, the graph of f(x) is concave down, since the slope of the graph is decreasing. After the inflection point, the slope of the graph is increasing, so it is concave up. Notice that the graph of f(x) is increasing over the entire interval; it is f'(x), or the slope of f(x), that determines the concavity of f(x). Whether the graph of f(x) itself is increasing or decreasing has no bearing on its concavity.
How to find an inflection point
In order to determine the position(s) of inflection point(s) given a function, it is necessary to be comfortable with computing derivatives as well as to understand the relationships between a function's first and second derivatives and concavity.
At points where f"(x) is positive, f'(x) is increasing, and f(x) is concave up. Similarly, when f"(x) is negative, f'(x) is decreasing, and f(x) is concave down. An inflection point occurs when the sign of the second derivative of a function, f"(x), changes from positive to negative (or vice versa) at a point where f"(x) = 0 or undefined. Thus, the process for determining the inflection points of a function are as follows:
- Compute the second derivative of the function.
- Solve for f"(x) = 0 or undefined; these are the points at which an inflection point can occur. Note that if a point is an inflection point, f"(x) = 0 or undefined. However, the opposite is not true, and it is necessary to test these points to determine whether they are inflection points or local extrema.
- Use the x-values from step 2 to divide the function into subintervals.
- Find the concavity of f(x) in the relevant subintervals: test values in the intervals before and after the points where f"(x) = 0 or undefined to determine whether f"(x) is changing sign before and after these points; if the sign is changing, the point is an inflection point as long as f(x) is continuous at the point.
Example
Find any inflection point(s) for the function:
1. Find f"(x):
2. Solve for f"(x) = 0:
3. Determine the relevant subintervals:
Since f"(x) = 0 at x = 0 and x = 2, there are three subintervals that need to be tested: (-∞, 0), (0, 2), and (2, ∞).
4. Test values within each subinterval:
| Subinterval | Sign of f"(x) at test value | Concavity |
|---|---|---|
| (-∞, 0) | (+) ; f"(-1) = 9 | Concave up |
| (0, 2) | (-) ; f"(1) = -3 | Concave down |
| (2, ∞) | (+) ; f"(3) = 9 | Concave up |
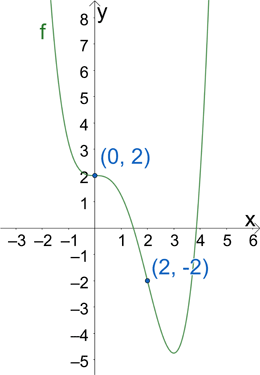
Since the concavity changes at both x-values, (0, 2) and (2, -2) are inflection points, as shown on the graph of f(x):
When f"(x) is undefined
An inflection point can also occur at points where f"(x) is undefined as long as the function, f(x), is continuous at that point and the concavity changes.
Example
Find any inflection point(s) for the function:
1. Find f"(x):
2. Solve for f"(x) = 0 or undefined:
There are no real solutions for f"(x) = 0, so instead we check for where f"(x) is undefined and find that f"(x) is undefined when x = -1:
3. Determine the relevant subintervals:
The only point at which f"(x) is undefined is x = -1, so we only need to consider points before and after x = -1. Thus, the intervals we need to test are (-∞, -1) and (-1, ∞).
4. Test values within each subinterval:
| Subinterval | Sign of f"(x) at test value | Concavity |
|---|---|---|
| (-∞, -1) | (+) ; f"(-2) = 2 | Concave up |
| (-1, ∞) | (-) ; f"(3) = -1/32 | Concave down |
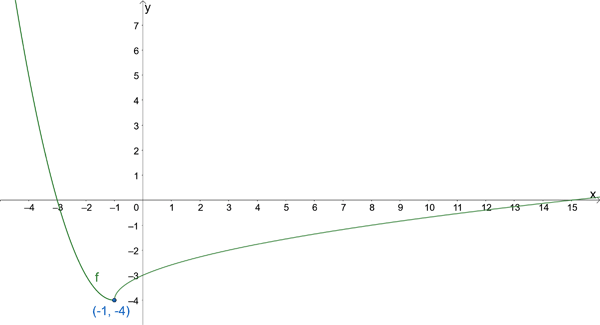
Since f(x) is continuous at x = -1, and the concavity changes from concave up to concave down, (-1, -4) is an inflection point, as shown in the graph of f(x):
When f(x) is not continuous
Note that for an inflection point to exist, f(x) must be continuous. Even if a point exists such that f"(x) = 0 or undefined, and concavity changes at that point, it is only an inflection point if f(x) is continuous at that point, as shown in the example below.
Find any inflection point(s) for the function:
1. Find f"(x):
| = | ||
| = | ||
| = | ||
| = |
2. Solve for f"(x) = 0 or undefined:
There are no real solutions for f"(x) = 0, so we instead determine where f"(x) is undefined. Since x = ±3 results in f"(x) having a denominator of 0, f"(x) is undefined at x = ±3.
3. Determine the relevant subintervals:
Since f"(x) is undefined at x = ±3, we need to test the following subintervals: (-∞, -3), (-3, 3), and (3, ∞)
4. Test values within each subinterval:
| Subinterval | Sign of f"(x) at test value | Concavity |
|---|---|---|
| (-∞, -3) | (+) ; f"(-4) = 114/343 | Concave up |
| (-3, 3) | (-) ; f"(0) = -2/81 | Concave down |
| (3, ∞) | (+) ; f"(4) = 114/343 | Concave up |
Because the concavity of f(x) changes at x = ±3, we might assume that -3 and 3 are inflection points. However, since f(x) is undefined at x = ±3, they cannot be inflection points. Below is a graph of f(x).
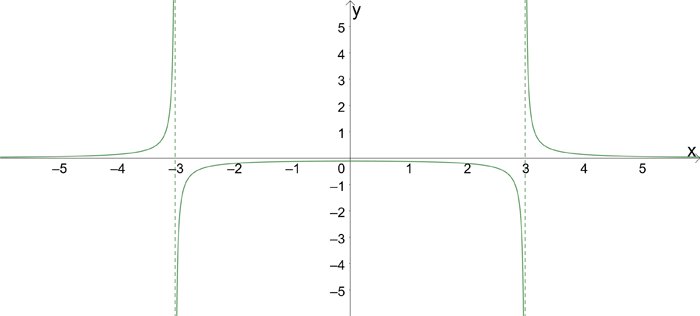
From the graph, we can see that vertical asymptotes occur at x = ±3, so no inflection point exists. This is one reason that it is important to pay attention to f(x). Based on the function, we could've determined at the beginning that f(x) is undefined at x = ±3. Then, after computing f"(x) and finding that f"(x) is undefined at the same values, we could've concluded without testing the intervals that f(x) has no inflection points.
Using f'(x) to find inflection points
Given a graph of f'(x), it is possible to find the inflection points of f(x) based on the relationships between f(x), f'(x), and f"(x):
- When f"(x) is positive, f'(x) is increasing, and f(x) is concave up.
- When f"(x) is negative, f'(x) is decreasing, and f(x) is concave down.
- When f"(x) is 0, f'(x) is not changing, and f(x) may have an inflection point, minimum, or maximum.
Given this information and a graph of f'(x), it is possible to determine the position of inflection points on f(x) by identifying points at which the graph of f'(x) changes from increasing to decreasing, or decreasing to increasing.
Example
Find any inflection point(s) for the function given the graph of f'(x).
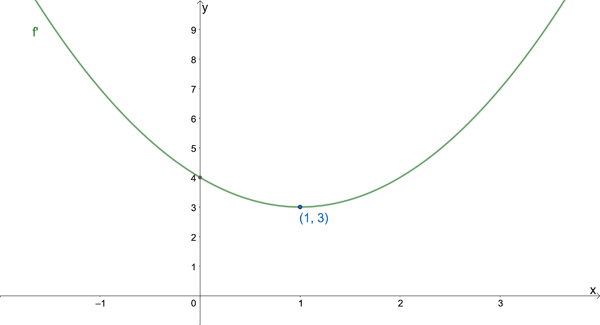
Since the graph of f'(x) changes from decreasing to increasing at the point (1, 3), there is an inflection point on the graph of f(x) at x = 1.
Although the process for finding inflection points can be simpler given a graph of f'(x), certain information needs to be provided for it to be possible, and we cannot determine the exact form of f(x) based on a graph of f'(x).
