Mean value theorem

The mean value theorem is considered to be one of the most important theorems in calculus because it is used to prove many other mathematical results. The mean value theorem is stated as follows. Given a function f(x) that is continuous over a closed interval [a, b] and is differentiable over an open interval (a, b), there exists at least one point c, where a < c < b, such that the instantaneous rate of change, f'(c), is equal to the average rate of change between the endpoints:

Consider the following graph of f(x), which is continuous over the interval [a, b], and is differentiable over (a, b).

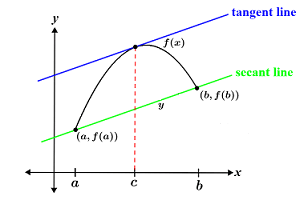
The average rate of change between the endpoints is the slope of the secant line formed between the endpoints, a and b. The slope of a line given two points is the ratio of the change in y to the change in x, so the slope of the secant line is . The instantaneous rate of change at a point c is the derivative of the function at that point, or geometrically, the slope of the tangent line at that point. The mean value theorem simply states that given the conditions of continuity and differentiability are met, there must be some point at which the slope of the tangent line shown in the figure is equal to that of the secant line. The mean value theorem cannot tell us where this point c is, only that it exists within the interval.

The mean value theorem is used throughout calculus to prove a number of mathematical results. It also has some important consequences, two of which are listed, but not proven, below:

1. Given that f(x) is continuous and differentiable over an interval I, if f'(x) = 0 for all x-values within the interval, then f(x) is constant (a horizontal line) over I.
2. Given that f(x) and g(x) are continuous and differentiable over an interval I, if f'(x) = g'(x) for all x-values within the interval, then f(x) = g(x) + C, where C is a constant within the interval. In other words, f(x) and g(x) are equivalent, but vertically offset functions.

Below are some examples of using the mean value theorem.

Example

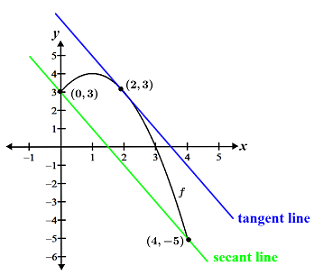
Find any x-values within the interval [0, 4] that satisfy the mean value theorem for f(x) = -x² + 2x + 3.

Since f(x) is a polynomial, it is continuous and differentiable over its entire domain. Thus, f(x) meets the conditions of the mean value theorem, and we can solve for x by taking the derivative of f(x) and setting it equal to the slope of the secant line between the endpoints:

The slope of the secant line is:

Setting f'(x) equal to m and solving for x,

-2x + 2	= -2
-2x	= -4
x	= 2

Thus, according to the mean value theorem, the slope of the line tangent to the curve at x = 2 is equal to the slope of the secant line between the endpoints, as shown in the figure below.

Given the appropriate conditions, the mean value theorem guarantees the existence of at least one point, c, that satisfies the conditions of the mean value theorem. However, it is possible for more than one point to satisfy the mean value theorem.

Example

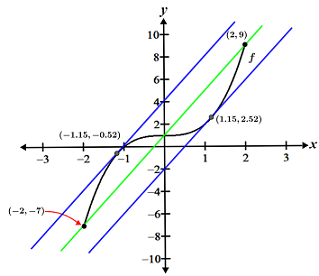
Find any x-values in the interval [-2, 2] that satisfy the mean value theorem for f(x) = x³ + 1

Since f(x) is a polynomial, it is continuous and differentiable over its entire domain. Thus, f(x) meets the conditions of the mean value theorem. The derivative of f(x) is:

The slope of the secant line is:

Setting f'(x) equal to m and solving for x,

Since both x = 1.15 and x = -1.15 are within the interval [-2, 2], both x-values satisfy the mean value theorem. It is worth noting that it is possible that an x-value does not lie within the interval of interest; in such a case, we would exclude said x-value because it must be within the interval to satisfy the mean value theorem. The graph of f(x) and the corresponding tangent lines are shown in the figure below: