Determinant
The determinant of an n x n square matrix A, denoted |A| or det (A) is a value that can be calculated from a square matrix. The determinant of a matrix has various applications in the field of mathematics including use with systems of linear equations, finding the inverse of a matrix, and calculus. The focus of this article is the computation of the determinant. Refer to the matrix notation page if necessary for a reminder on some of the notation used below. There are a number of methods for calculating the determinant of a matrix, some of which are detailed below.
Determinant of a 2 × 2 matrix
The determinant of a 2 × 2 matrix, A, can be computed using the formula:
,
where A is:
One method for remembering the formula for the determinant involves drawing a fish starting from the top left entry a. When going down from left to right, multiply the terms a and d, and add the product. When going down from right to left, multiply the terms b and c, and subtract the product.
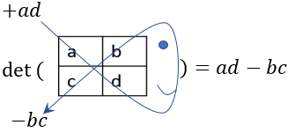
This method and formula can only be used for 2 × 2 matrices.
Example:
Find the determinant of :
|A| = (1)(4) - (-3)(2) = 4 + 6 = 10
Note that if a matrix has a determinant of 0, it does not have an inverse. Thus, it can be helpful to find the determinant of a matrix prior to attempting to compute its inverse.
Determinants of larger matrices
There are a number of methods used to find the determinants of larger matrices.
Cofactor expansion
Cofactor expansion, sometimes called the Laplace expansion, gives us a formula that can be used to find the determinant of a matrix A from the determinants of its submatrices.
We define the (i,j)th submatrix of A, denoted Aij (not to be confused with aij, the entry in the ith row and jth column of A), to be the matrix left over when we delete the ith row and jth column of A. For example if i = 2 and j = 4, then the 2nd row and 4th columns indicated in blue are removed from the matrix A below:
resulting in matrix Aij:
The i-jth cofactor, denoted Cij, is defined as . This definition gives us the formula below for the determinant of a matrix A:
Be careful not to confuse Aij, the (i,j)th submatrix, with aij, the scalar entry in the ith row and the jth column of A. This formula is called the "cofactor expansion across the ith row." Notice that in this formula, j is changing but i remains fixed. This represents moving across the ith row and adding and subtracting the current entry, aij, times the current cofactor Cij in an alternating pattern.
Similarly, the cofactor expansion formula down the jth column is
Example
When performing cofactor expansion, it is very useful to expand along rows or columns that have many 0's since if aij = 0, we won't have to calculate because it will just be multiplied by 0. This greatly reduces the number of steps needed. Below, blue represents the column or row we are expanding along.
Using the formula for calculating the determinant of a 2 × 2 matrix:
Given that the matrix is square, cofactor expansion can be used to find the determinants of larger square matrices as shown above. The bigger the matrix however, the more cumbersome the computation of the determinant.
Gaussian elimination
Gaussian elimination, also referred to as row reduction, is a process that "reduces" a matrix into a simplified form that enables us to do things such as find the determinant or solve a system of linear equations. It involves converting a matrix through a series of row operations into a matrix that can be worked with more easily. For the purpose of using Gaussian elimination to find the determinant, we want to convert a given matrix into either an upper or lower triangular matrix.
A square matrix in which the entries below the main diagonal are all 0 is referred to as an upper triangular matrix; if all the entries above the main diagonal are all 0, the matrix is referred to as a lower triangular matrix:
| Upper triangular matrix | Lower triangular matrix |
Given that A is a square, triangular matrix, its determinant is the product of its diagonal entries:
Conducting certain row operations (refer to the matrix page for reference) on a matrix, A, alters the matrix such that the determinant of the altered matrix, B, is affected as follows:
- When two rows of A are switched, det(B) = -det(A), or det(A) = -det(B)
- When A is multiplied by a scalar, c, det(B) = c·det(A)
- When some row (or multiple of a row) of A is added (combined) with some other row of A to form a new row, the determinant doesn't change, so det(B) = det(A)
Example
Find the determinant of A by using Gaussian elimination (refer to the matrix page if necessary) to convert A into either an upper or lower triangular matrix.
Step 1: R1 + R3 → R3:
Based on iii. above, there is no change in the determinant.
Step 2: Switch the positions of R2 and R3:
Switching the position of two rows changes the sign of the determinant (i.), so we added a negative sign.
Step 3: -¼R2 + R3 → R3
The matrix is now in upper triangular form, so the determinant can be computed as the product of its main diagonal:
Properties of determinants
Below are some properties of determinants of square matrices.
, where I is the identity matrix
- A square matrix, A, is invertible only if
- If one row of A is a multiple of another row, then
, and A is referred to as a singular matrix
Below are some examples of these properties in use.
Property i. For and
, show that
Property ii. For , show that
:
Property iii. For
| and |
we can show that:
Thus:
Next, find det(AB):
Property iv. For the identity matrix , show that
.
Property v. Because the process of finding the inverse of a square matrix always involves a factor of , the determinant of A cannot be 0, because that would make
undefined. For
:
Property vi. For , in which R3 = 2R2,
which confirms property vi.
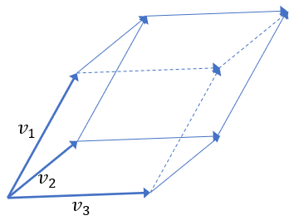
Geometric meaning of a determinant
The determinants a number that represents the "signed volume" of the parallelepiped (the higher dimensional version of parallelograms) spanned by its column or row vectors. The term "signed volume" indicates that negative volume is possible in cases when the parallelepiped is turned "inside out" in some sense. For example, if we switch 2 vectors of the parallelepiped, we are essentially pushing 2 of the sides past each other until the interior of the parallelepiped faces outwards and the former exterior now faces inwards. In 3D, a parallelepiped spanned by vectors v1, v2, and v3 looks like a slanted box: