Matrix multiplication

Matrix multiplication can either refer to multiplying a matrix by a scalar, or multiplying a matrix by another matrix. If necessary, refer to the matrix notation page for a review of the notation used to describe the sizes and entries of matrices.

Matrix-Scalar multiplication

The first kind of matrix multiplication is the multiplication of a matrix by a scalar, which will be referred to as matrix-scalar multiplication. A scalar is a number that makes things larger, smaller, or even negative (think of a negative scalar as "pointing backwards" or "flipping" something in the opposite direction). Given an m × n matrix, A, and a scalar, c, the matrix, cA, or Ac, is the m × n matrix whose i,jth entry is c times the i,jth entry of A. In other words,



for all i=1, ..., m and j = 1, ..., n. For example,




Properties of Matrix-Scalar multiplication



Matrix-Matrix multiplication

Multiplying two matrices involves the use of an algebraic operation called the dot product. A vector can be seen as a 1 × matrix (row vector) or an n × 1 matrix (column vector). To use the dot product, the vectors must be of equal length, meaning that they have the same number of entries. Given two matrices, A and B, if



and



the dot product of A and B is:



Note that in the equation above, the "·" represents the dot product, not multiplication. To multiply matrices, the dot product of the corresponding rows and columns of the matrices being multiplied are computed to determine the entries of the resulting matrix; this is described in detail below.

It follows that, in order to multiply two matrices, A and B, the number of columns of A must equal the number of rows of B. For a product matrix, AB, to be defined in general, A must be m × n, and B must be n × p for some positive integers m, n, and p. If A is m × n, and B is n × p, the product matrix, AB, is the m × p matrix such that the i,jth entry of AB, denoted (AB)ij, is the dot product of the ith row vector of A



with the jth column vector of B



Therefore, (AB)ij is given by the formula:


   = 
     = 
     = 

for all i = 1,2 ..., m and j = 1,2, ..., p (i runs through the rows of A, of which there are m, and j runs through the columns of B, of which there are p). The row and column highlighted in blue in the matrices below represent the ith row and jth column of the matrices being multiplied:



Thus, the (AB)ij entry is the sum of the products of the entries of row i of matrix A and column j of matrix B:



Example

Multiply A and B if A is the following 2 × 3 matrix and B is the following 3 × 2 matrix:


  


   = 
     = 
     = 
     = 

corresponds to:



   = 
     = 
     = 

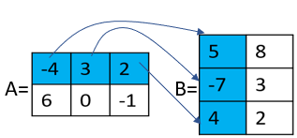
corresponds to:



   = 
     = 
     = 
     = 

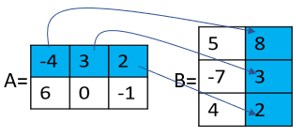
corresponds to:



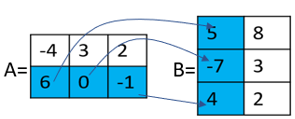
and


   = 
     = 
     = 
     = 

corresponds to:



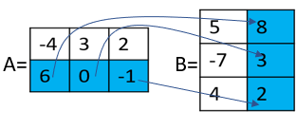
Assembling these entries into the matrix product AB yields


 
 

However, if instead,


  


then AB is not defined since A has 3 columns and B has 2 rows, and 3 ≠ 2.


Properties of matrix multiplication