Matrix notation
This page summarizes the notation commonly used when working with matrices.
Matrix Dimensions
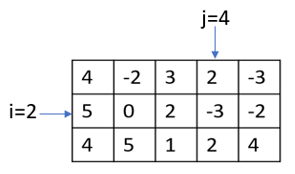
Whenever we say "A is an m by n matrix," or simply "A is m x n," for some positive integers m and n, this means that A has m rows and n columns. Matrix A below is an example of a 3 x 5 (three by five) matrix:
Vectors
A vector can be seen as either a 1 x n matrix in the case of a row vector, or an n x 1 matrix in the case of a column vector. Below, v is a 3 x 1 column vector and w is a 1 x 4 row vector.
Column vectors are much more commonly used than row vectors.
Linear combinations
A linear combination of vectors, v1, ..., vn is any vector of the form
x1v1 + ... + xnvn
for some numbers x1, ..., xn. For example, the vector,
is a linear combination of:
because
or
ℝn and standard basis vectors
If n is any positive integer, an n-dimensional vector with real entries is called an n-vector, and the set of all n-vectors is called n-dimensional space, n-space, or ℝn. For example, ℝ3 consists of all 3-vectors of the form
where a, b, and c are real numbers. In ℝn, we define ei for all i = 1, 2, ... n as the column vector with a 1 in the ith position (counting from the top-down) and 0 everywhere else. For example, in ℝ3,
The ei's are called the standard basis vectors of ℝn because any n-vector in ℝn can be represented as a linear combination of the standard basis vectors. For example, in ℝ3, the vector
can be represented as
or
Matrices as collections of rows and columns
Often, it is useful to think about an m × n matrix A as a collection of its n column vectors, each of which has m dimensions. For example, the 3 × 4 matrix,
can be viewed as the following set of 4 vectors, each of 3 dimensions.
Here, the curly braces, {}, are being used to denote a set of objects. If the column vectors of A are v1, ..., vn in that order, then we can represent A as,
, where
which we write as A = [v1 v2 ... vn]. Similarly, we can also view A as the collection of its m row vectors, each of which has n dimensions. If the row vectors of A are r1, ..., rm in that order, then we can represent A as
, where
Thus, matrix A can be represented as the following set of row vectors:
Entries of a matrix
Each number inside a matrix is called an entry. To refer to a specific entry of a matrix we use the i,jth notation: for some positive integers i and j, the i,jth entry of a matrix A, denoted ai,j is the entry in the ith row of the jth column. We always count rows from top to bottom and columns from left to right.
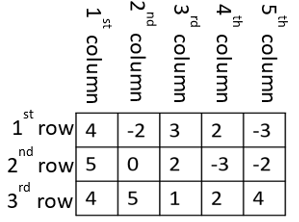
In the matrix above, if i = 2 and j = 4, the i,jth entry would be -3.