Direct variation
Direct variation refers to a relationship between two variables where when one variable increases the other also increases by the same factor. Conversely, when one variable decreases, the other variable also decreases by the same factor. As such, the ratio between two variables that are in direct variation (or directly proportional) always remains the same.
Variables in direct variation can be modeled by the equations
or
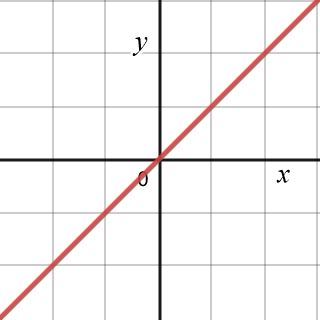
where k is a constant of proportionality, and x ≠ 0. The graph of two variables in direct variation is simply a straight line through the origin, as shown in the figure below, using the graph of y = 1x. In the graph we can see that as x increases, y also increases, and as x decreases, y also decreases.
There are many examples of variables in the real world that are in direct variation, such as the gallons of gasoline pumped into a car, and the cost of the gasoline. The more gasoline that is pumped into the car, the higher the cost; the less gasoline pumped, the lower the cost. The rate at which a plant grows is another example.
Example
Given that a plant's height is in direct variation with its age, it grows 4 inches for every elapsed week, and its height is 0 (planted seed) at the beginning of the first week, determine how tall the plant will be by the end of 4 weeks, noting its height with each passing week.
Since it is given that the two variables, height and age, are in direct variation, we can use the equation for direct variation:
The constant of proportionality, k, is 4, the age of the plant is x, and the height of the plant is y. The height of the plant at the end of each week can therefore by found by multiplying its age by 4:
 |
y = 4x
|
Because we can see that the plant's height increases at the same rate as its age, we can confirm that x and y are in direct variation. More specifically, we can see that x and y increase at the same rate. When x is doubled, y also doubles. When x is tripled, y also triples, and so on. Furthermore, the ratio between x and y remains constant, as y is always 4 times x. This is what is meant when someone says that x and y are in direct variation, y varies directly with x, or y is directly proportional to x; they all mean the same thing.
