Inverse variation
Inverse variation refers to a relationship between two variables where when one variable increases, the other decreases by the same factor, assuming that all other variables remain equal. Variables that exhibit this relationship are described as being "in inverse variation" or "inversely proportional." Both have the same meaning. In other words, the product of variables that are in inverse variation is constant, and their relationship can be modeled by the equations
or
where k is a constant of proportionality, x ≠ 0, and y ≠ 0. The graph of two variables in inverse variation is a hyperbola, as shown in the figure below using the graph of y = 1/x. In the graph, we can see that as x increases, y decreases, and vice versa.
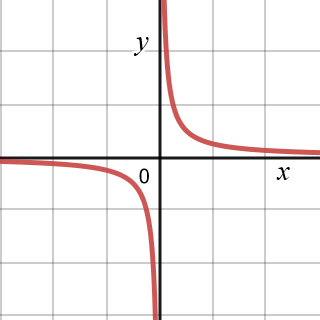
There are many examples of variables in the real world that are in inverse variation, such as speed and time as they relate to travel over a constant distance. The faster a person travels, the less time it takes for them to travel a certain distance; the slower they travel, the longer it takes them to travel that same distance. Another common example is the amount of time it takes some number of people to complete a task.
Example
If it takes 1 student 5 minutes to complete an assignment, and the amount of time it takes the student(s) to complete the assignment is in inverse variation with the total number of people, determine the amount of time it will take 2, 3, and 4 people to complete the assignment.
Since it is given that the two variables are in inverse variation, we can use the equation for inverse variation:
The constant of proportionality, k, is 5, x is the number of people, and the time it takes them to complete the assignment is y. Dividing the constant of proportionality by 2, 3, and 4 students tells us how many minutes it will take them to complete the assignment:
 |
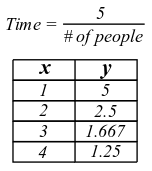
|
Because we can see that increasing the number of people decreases the amount of time it takes to complete the assignment, we can confirm that x and y are in inverse variation. More specifically, when x is doubled, y is halved. When x is increased by a factor of 3, y is decreased by a factor of 3, and so on. This is what is meant when someone says that x and y are in inverse variation, y varies inversely with x, or y is inversely proportional to x; they all mean the same thing.
