home / calculus / integral / fundamental theorem of calculus

Fundamental theorem of calculus

The fundamental theorem of calculus (FTC) establishes the connection between derivatives and integrals, two of the main concepts in calculus. It also gives us an efficient way to evaluate definite integrals. Consider the following figure:

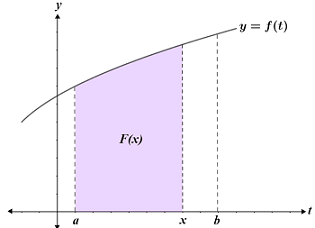
Given a function f(t) that is continuous over an interval [a, b], recall that an integral represents the area under the curve. In the figure, F(x) is a function that represents the area under the curve between a and some point x within the interval. In other words, the area under the curve is represented by:

Note that even though F(x) is defined in terms of the integral of another function, which may seem confusing since we expect a definite integral to be a number, the result of the integral for any given x value is indeed a number. In this case, t is simply a placeholder that allows us to avoid confusion that could otherwise result from using x in both the bounds of the integral as well as the integrand since for all values of x, F(x) is dependent only on x, not t. Given the above, the first part of the fundamental theorem of calculus states:

Fundamental theorem of calculus, part 1

Let f be a continuous function over the interval [a, b], and let F be a function defined by

Then, F is continuous over [a, b], differentiable over (a, b), and

over (a, b).

This is important because it connects the concepts of derivatives and integrals, namely that derivatives and integrals are inverses. The FTC also implies that any continuous function, f, has an antiderivative, F(x). The second part of the fundamental theorem of calculus provides an efficient way to evaluate definite integrals, rather than needing to approximate area using Riemann sums.

Fundamental theorem of calculus, part 2

Let f be a continuous function over the interval [a, b] and let f(x) have an antiderivative F(x) over the interval (a, b) such that F'(x) = f(x). Then:

In other words, if we can find an antiderivative for the integrand, the fundamental theorem of calculus allows us to evaluate the definite integral by subtracting the values of the antiderivatives at the endpoints of the interval.

Example

Evaluate the following integral:

From the FTC, if we can find a function F that satisfies F'(x) = x², then:

One such F that satisfies F'(x) = x² is

so:

The FTC and chain rule

Recall from the first part of the fundamental theorem of calculus that:

Using this fact along with the chain rule, it is possible to find the derivatives of various functions.

Example

Find the derivatives of the following functions.

Notice that the upper bound of the definite integral is x² instead of x, so to set up the chain rule, we make the substitution u = x². The chain rule implies that:

		=
		=

Then, using the first part of the fundamental theorem of calculus,

		=
		=

and so

		=
		=

This problem could potentially cause confusion since we have the independent variable, x, mixed in with the placeholder variable, t, under the integral, and differentiating or integrating with respect to the wrong variable would result in the wrong answer. However, since the integral is with respect to t because of the dt term, the x² term can be treated as constant, so we can factor it out of the integral to get

Now we can use the product rule to find :

and , so

Proof of the fundamental theorem of calculus

Suppose f(x) is continuous on [a, b]. Then F is a function that satisfies F'(x) = f(x) if and only if

for all x in [a, b].

To prove that if , then , we first assume that

for all x in [a, b]. Adding F(a) to both sides gives us an expression for F(x):

(1)

The limit definition of F'(x) is:

Refer to the derivatives page for more information on the limit definition of a derivative.

Plugging equation (1) into the limit definition of a derivative,

As h becomes smaller, x + h approaches x, or more formally, . By continuity of f, , so as h goes to 0, the function values f(t) for all t in the interval x ≤ t ≤ x + h also satisfy , so

Now to prove that if F'(x) = f(x) then , we assume that F'(x) = f(x) for all x in [a, b]. This also means that when we fix an x in [a, b],

for all t in the interval a ≤ t ≤ x. Plugging the above substitution into the integral gives

(2)

We can break the interval [a, x] into n intervals [a, a + h], [a + h, a + 2h],..., [a + (n - 1)h, a + nh] where . This sets us up for viewing the right side as the limit of Riemann sums:

(3)

where each t_i is a random value in the ith interval [a + (i - 1)h, a + ih]. By the Mean Value Theorem, there exists a t_i^* in the ith interval [a + (i - 1)h, a + ih] that satisfies

Since the t_i's are randomly chosen, we can replace each t_i with t_i^*, so the limit of the Riemann sums becomes

(4)

On the right side, after canceling the h's, we get the telescoping series:

From extrapolating the above, we see that all the middle terms cancel out, leaving only F(a + nh) and F(a) at the beginning and end of the telescoping sum. Also note that

Therefore:

(5)

Chaining together the series of substitutions given by (2) - (5), we get

whenever F'(x) = f(x) for all x in [a, b].