Derivative
The derivative of a function is the rate of change of the function's output relative to its input value. Given y = f(x), the derivative of f(x), denoted f'(x) (or df(x)/dx), is defined by the following limit:
The definition of the derivative is derived from the formula for the slope of a line. Recall that the slope of a line is the rate of change of the line, which is computed as the ratio of the change in y to the change in x. Geometrically, the derivative is the slope of the line tangent to the curve at a point of interest. It is sometimes referred to as the instantaneous rate of change. Typically, we calculate the slope of a line using two points on the line. This is not possible for a curve, since the slope of a curve changes from point to point. Consider the figure below.
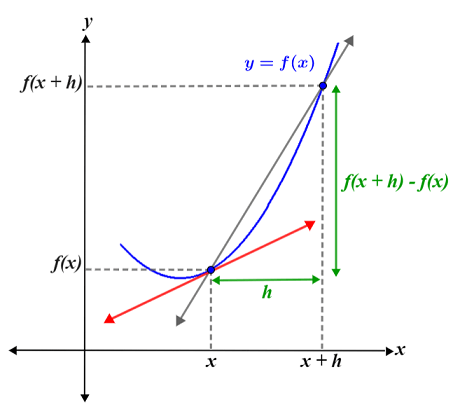
The figure shows a curve (blue) with two points: (x, f(x)) and (x + h, f(x + h)). The grey secant line represents the slope between these two points and is computed as:
Notice that this is beginning to look like the definition of the derivative. However, this formula gives us the slope between the two points, which is an average of the slope of the curve. The derivative at x is represented by the red line in the figure. To calculate the slope of this line, we need to modify the slope formula so that it can be used for a single point. We do this by computing the limit of the slope formula as the change in x (Δx), denoted h, approaches 0. By doing this, we find the slope between two points separated by a difference so small that it provides an approximation for the slope at a single point, leading us to the definition of the derivative stated above.
Examples
Use the limit definition of a derivative to differentiate (find the derivative of) the following functions.
1. f(x) = x2:
Thus, the derivative of x2 is 2x. To find the derivative at a given point, we simply plug in the x value. For example, if we want to know the derivative at x = 1, we would plug 1 into the derivative to find that:
f'(x) = f'(1) = 2(1) = 2
2. f(x) = sin(x):
To solve this problem, we will use the following trigonometric identities and limits:
| (1) | |
| (2) | |
| (3) |
The points at which the above identities and limits are applied will be denoted using their respective identifiers: (1), (2), and (3).
Thus, the derivative of sin(x) is cos(x), or:
Table of derivative rules
Notice from the examples above that it can be fairly cumbersome to compute derivatives using the limit definition. Fortunately, the rules for computing the derivatives for different types of functions are well-defined, so simply knowing (or being able to reference) these rules enables us to differentiate most functions.
| Function: f(x) | Derivative: f'(x) |
|---|---|
(power rule) |
|
for some constant a > 0 and a ≠ 1 |
|
for some constant a > 0 |
|
for any constant c and function f |
|
for any functions f and g |
|
product rule |
|
quotient rule |
|
the |
chain rule |
Undefined derivatives
It is not always possible to find the derivative of a function. In some cases, the derivative of a function may fail to exist at certain points on its domain, or even over its entire domain. Generally, the derivative of a function does not exist if the slope of its graph is not well-defined. Below are some of these cases.
Discontinuous functions
For a function to have a derivative at a given point, it must be continuous at that point. A function that is discontinuous at a point has no slope at that point, and therefore no derivative. Briefly, a function f(x) is continuous at a point a if the following conditions are met:
- f(a) is defined.
.
.
The figure below shows one type of discontinuity, referred to as a jump discontinuity, at the point x = 3.
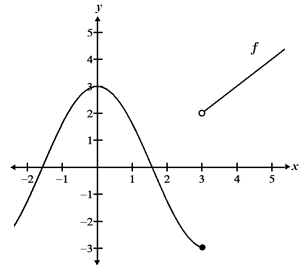
Since the function is discontinuous at this point, it does not have a derivative at x = 3.
Cusps/corners
Functions with cusps or corners do not have defined slopes at the cusps or corners, so they do not have derivatives at those points. This is because the slope to the left and right of these points are not equal.
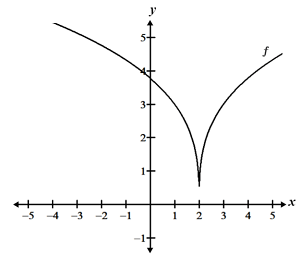
|
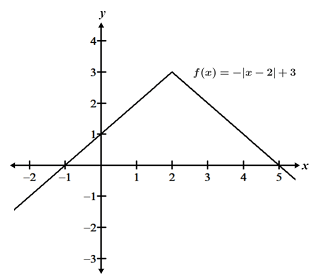
|
| Cusp | Corner |
Both functions have either a cusp or a corner at x = 2, where the slope of the function differs depending on whether we approach the point from the left or the right side. Thus, the derivative is undefined at x = 2.
Vertical tangents or infinite slope
A function that has a vertical tangent line has an infinite slope, and is therefore undefined.
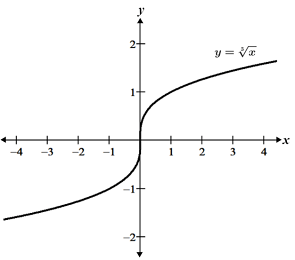
The function has a vertical tangent at x = 0. On either side of the vertical tangent, the slope of the function approaches infinity.
Did you know??
The Weierstrass function is continuous everywhere but differentiable nowhere! The Weierstrass function is "infinitely bumpy," meaning that no matter how close you zoom in at any point, you will always see bumps. Therefore, you will never see a straight line with a well-defined slope no matter how much you zoom in.

