2D
In geometry, a dimension can be defined as the minimum number of coordinates necessary to specify a point within a mathematical space. Based on this definition, a two-dimensional object is an object in which a point on the object can be specified using 2 coordinates; in other words, the object has 2 separate dimensions that can be measured, as opposed to a 1D object such as a line, where only one dimension can be measured.
A two-dimensional (2D) object is often described as having length and width, but no depth/thickness. 2D objects are also referred to as 2D shapes, 2D figures, plane figures, and more. The study of 2D objects is also referred to as plane geometry, and as the name suggests, plane geometry deals with objects that lie entirely within one plane.
Types of 2D objects
There are many different types of 2D objects. Two broad categories of 2D objects are polygons and curved shapes.
Polygons
Polygons are a type of closed (all the segments form a closed boundary) shape formed by a finite number of straight line segments. A square, hexagon, and pentagon are a few examples of polygons.
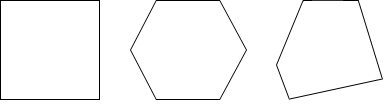
All of the above are formed only using straight line segments: a square has 4, a hexagon has 6, and a pentagon has 5. In general an n-gon is made up of n line segments, or sides. Polygons can be further distinguished into many different categories.
Curved shapes
Curved objects are another type of 2D object. They may or may not be closed objects, and not all of their "sides" need to be curved to be considered a curved object. The circle, ellipse, and other objects below are just a few examples.
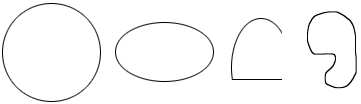
Regardless of the type of object (curved, polygon, etc.), to be classified as a 2D object, the object must lie entirely within one plane and can only be measured in 2 different dimensions. When a third dimension exists, we are instead dealing with 3D objects and what is referred to as solid geometry.
Coordinate geometry
Coordinate geometry, also referred to as analytic geometry or Cartesian geometry is the study of geometry in the context of a coordinate system. In two dimensions, a Cartesian coordinate system is referred to as a rectangular (or orthogonal) coordinate system. It is comprised of two perpendicular number lines referred to as axes such that both axes share the same unit of length. The position of a point in the coordinate plane is given by an ordered pair of numbers (x1, y1), where x1 indicates horizontal position and y1 indicates vertical position, as shown in the figure below.
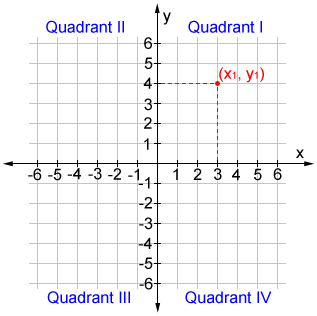
Coordinate geometry enables us to define shapes numerically, which in turn allows us to use other mathematical concepts such as algebra to formulate equations that we can use to study shapes and solve problems. For example, the distance formula can be used to determine the lengths of the sides of a shape if the points at the vertices of the shape are known.
Other dimensions
In geometry, we usually consider 0-dimensional, 1-dimensional, 2-dimensional, and 3-dimensional space.
0D
A point is a 0D object; it has no dimensions, only a position in space.

Of course, a point on a page (like the one above) does have some dimension, since for practical purposes, we have to use something to represent 0D.
1D
A one-dimensional object only has 1 dimension. Usually, this dimension is length. A line, ray, or line segment, are all examples of 1D objects. Only one coordinate (3) is necessary to specify the position of point A on the number line below.

3D
A cube is a 3D object; it has length, width, and height. The dotted lines represent the 3 dimensions of the cube, which shows that 3 coordinates are necessary to specify the position of point A within the cube.

