1D
In geometry, a dimension can be defined as the minimum number of coordinates necessary to specify a point within the mathematical space. Based on this definition, a one-dimensional (1D) object is an object in which a point on the object can be specified using just 1 coordinate.
A 1D object is often described as an object that has a length, but no height, width, or depth/thickness. Examples of objects in geometry that fit this definition include lines, rays, and line segments. Lines extend infinitely, rays have one endpoint and one end that extends infinitely, and line segments have two endpoints. All of them share the characteristic of only having the dimension of length, at least in theory. Realistically, the lines, rays, and line segments shown below have some width, albeit small. A truly one-dimensional line is something we wouldn't be able to see on the page since it would have no thickness.

A number line is another of example of a common mathematical object that is one dimensional. It is one dimensional because only one coordinate needs to be specified to identify a specific position on the number line. For example, "6" refers to the position 6 tick marks to the right of 0. Any number we state will be some distance left or right on the number line. We cannot specify a position above, below, or anywhere else, because there is only one dimension.
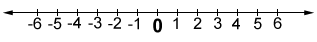
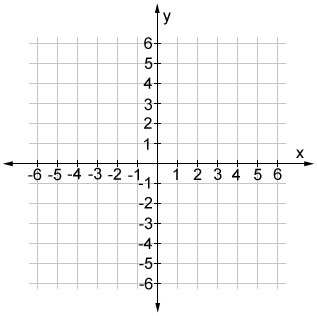
Similarly, the x-axis and y-axis on a coordinate plane are one dimensional when considered individually. Together however, they make up a two-dimensional coordinate plane.
Other dimensions
In geometry, we usually consider 0-dimensional, 1-dimensional, 2-dimensional, and 3-dimensional space.
0D
A point is a 0D object; it has no dimensions, only a position in space.

Of course, a point on a page like the one above does have some dimension, since for practical purposes, we have to use something to represent 0D.
2D
A square is a 2D object; it has length and width. To specify the point A on the square, we need 2 coordinates, not just 1, as we would on a line. The dotted lines represent the 2 dimensions of the square, which shows that 2 coordinates are necessary to specify the position of point A within the square.

3D
A cube is a 3D object; it has length, width, and height. The dotted lines represent the 3 dimensions of the cube, which shows that 3 coordinates are necessary to specify the position of point A within the cube.

Did you know??
In mathematics, higher dimensions may be discussed, but the world we live in is three dimensional, so while we may come across 2D or 1D objects, we can't really perceive higher dimensions.
