Distance formula
The distance formula is a formula that determines the distance between two points in a coordinate system.
Distance formula for a 2D coordinate plane:
Where (x1, y1) and (x2, y2) are the coordinates of the two points involved.
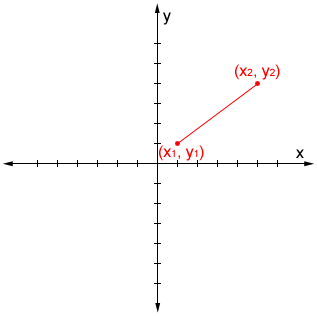
Example:
Find the length of line segment AB given that points A and B are located at (3, -2) and (5, 4), respectively.
| d = | |
| = | |
| = | |
| = | |
| = |
Distance formula for a 3D coordinate plane:
Where (x1, y1, z1) and (x2, y2, z2) are the 3D coordinates of the two points involved.
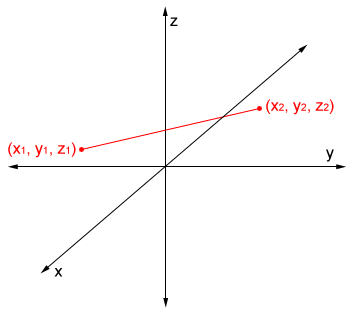
Other coordinate systems exist, but this article only discusses the distance between points in the 2D and 3D coordinate planes.
The Pythagorean Theorem and the distance formula
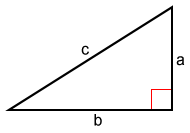
The distance formula can be derived from the Pythagorean Theorem. The Pythagorean Theorem says that the square of the hypotenuse equals the sum of the squares of the two legs of a right triangle. Referencing the right triangle sides below, the Pythagorean theorem can be written as:
c2 = a2 + b2
Given two points, A and B, with coordinates (x1, y1) and (x2, y2) respectively on a 2D coordinate plane, it is possible to connect the points with a line and draw vertical and horizontal extensions to form a right triangle:
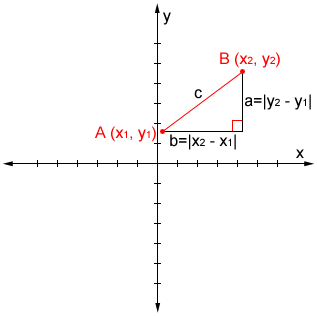
The hypotenuse of the right triangle, labeled c, is the distance between points A and B. The horizontal and vertical distances between the two points form the two legs of the triangle and have lengths |x2 - x1| and |y2 - y1|.
Using the Pythagorean Theorem:
c2 = |x2 - x1|2 + |y2 - y1|2
We can rewrite this using the letter d to represent the distance between the two points as
which is the distance formula between two points on a coordinate plane.
In a 3D coordinate plane, the distance between two points, A and B, with coordinates (x1, y1, z1) and (x2, y2, z2), can also be derived from the Pythagorean Theorem.
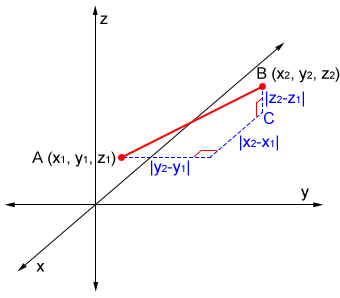
Referencing the above figure and using the Pythagorean Theorem, AC2 = (x2 - x1)2 + (y2 - y1)2. Triangle ACB is also a right triangle, so
| AB = | |
| = |
AB is the distance between the two points, so
