Geometry

Geometry is a branch of mathematics that includes the study of shape, size, and other properties of figures. It is one of the oldest branches of mathematics and may have been used even in prehistoric times. We can produce geometric figures from real-life situations. Below is a picture where points, lines, and planes represent the walls and structural components of buildings.

Geometry is often divided into plane geometry and solid geometry.

Plane Geometry

Plane geometry includes the study of points, lines, and geometric figures such as circles and polygons that lie in a plane.

There are three terms in geometry that are widely used that cannot really be defined using well-defined objects. There is however, a general agreement as to what they mean; that is, the definitions of these terms are axiomatic. They are the basis for creating and working with any geometric figure.

Point

A point indicates a location in space. It has no dimension and is represented by a dot. Points are typically labeled with capital letters.

• A
point A

Line

A line has one dimension, its length, and is represented with a line containing arrows indicating it extends in either direction indefinitely. Two non-overlapping points determine a unique line and we can name the line with those two points or any other two points on the line.

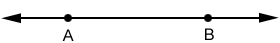
line AB or BA

Plane

A plane has two dimensions, length and width, and forms a flat surface (such as a piece of notebook paper) extending in both directions indefinitely. A plane can be named by three noncollinear points or by a letter.

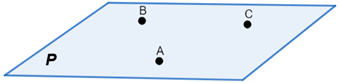
Plane ABC or plane P

The shapes formed in plane geometry have perimeter and area if they are polygons, circumference and area if they are circles, and length if they are one dimensional, like a line.

Solid Geometry

Solid geometry is the branch of geometry that studies solid (three-dimensional) figures. The solids are polyhedra (plural for polyhedron) or non-polyhedra.

Polyhedron

A polyhedron is a solid whose faces are polygons.

Octahedron whose faces are triangles		Rectangular prism whose faces are rectangles.

Non-polyhedron

A non-polyhedron is a solid that has all or partly curved surfaces.

A right cone has a circular base that tapers to a tip.		A sphere's surface is completely round like a ball.

The shapes formed in solid geometry have volume and surface area. You can also measure the length for a part of a solid such as the length of an edge of a rectangular prism or the radius of a sphere.

Types of Geometry

There are numerous branches of geometry that are classified based on various criteria such as the methods of study, the types of objects studied, and more. The following are some of said branches:

Analytic Geometry

Analytic geometry is the study of plane and solid geometry that uses Algebra and incorporates the two-dimensional coordinate plane or three-dimensional coordinate plane. It is sometimes referred to as coordinate geometry for this reason.

Since analytic geometry uses Algebra and the coordinate planes for geometric figures, it tends to be more numerical in nature, and thus has proven to be an important branch of mathematics used by engineers and physicists.

Euclidean Geometry

Euclidean geometry is the study of plane and solid geometry which uses axioms, postulates, and deductive reasoning to prove theorems about geometric concepts.

Non-Euclidean Geometry

Non-Euclidean geometry typically uses most of the ideas of Euclidean geometry but uses a different version of Euclid's parallel postulate. In Euclidean geometry two parallel lines never intersect. In Non-Euclidean geometry, parallel lines can intersect depending on which type of geometry is chosen. There are two basic types: Spherical and Hyperbolic Non-Euclidean geometries.

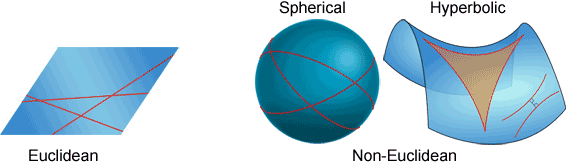
Think of folding a plane in Euclidean geometry onto a sphere or a hyperboloid (a three-dimensional hyperbola). The lines are bent and circular or elliptical in spherical geometry, and parabolic or hyperbolic in hyperbolic geometry.