Basic set operations
In mathematics, a set is a collection of well-defined and distinct objects, where an object is something that is, or can be, formally defined. Numbers, integers, permutations, combinations, functions, points, lines, and segments are just a few examples of mathematical objects.
Set theory can be used in deductive reasoning and mathematical proofs, and as such, can be seen as a foundation through which most math can be derived.
There are four basic operations in set theory: unions, intersections, complements, and Cartesian products.
Unions
Unions are a result of "adding" two sets together. Unions are denoted by the symbol "∪."
The union of two sets, A and B, written A ∪ B, includes all objects that are members of A, B, or both.
Example:
Given the following sets:
| A = {4, 5, 6} |
| B = {6, 7, 8} |
| A ∪ B = {4,5,6} ∪ {6,7,8} = {4,5,6,7,8} |
Below is a depiction of a union of two sets:
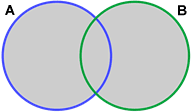
The shaded grey area represents the union of A and B.
Intersections
Intersections are the result of determining the common members between two sets. Intersections are denoted as "∩."
The intersection of two sets, A and B, written A ∩ B, includes all objects that are in both A and B.
Example:
Given the following sets:
| A = {4, 5, 6} |
| B = {6, 7, 8} |
| A ∩ B = {4,5,6} ∩ {6,7,8} = {6} |
Below is a depiction of the intersection of two sets:
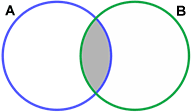
The shaded grey area represents the intersection of A and B.
Complements
The complement of a set, A, refers to the elements that are not in A. Among other notations, the complement of A can be denoted as Ac. For example, in a case where all integers are being considered, if A were the set of all even integers, Ac would be the set of all odd integers.
Sets can be "subtracted." The difference between two sets, A and B, can be denoted as A \ B. This difference can be referred to as the relative complement of B in A and represents the set of all elements in A that are not in B. This difference can be depicted as follows:
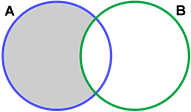
In the context of complements, a universal set, U, can be said to contain all the subsets being discussed. In such a case, U \ A would be the complement of A. In other words, Ac = U \ A.
Below is a depiction of Ac:

The grey area represents the complement of A.
Cartesian products
Cartesian products are the set of all ordered pairs, (a, b), where a and b are members of the sets A and B respectively. Cartesian products make it possible to construct a new set by associating each element in one set with each element in another set. Cartesian products can be denoted as A x B.
Example:
Given the following sets:
| A = {4, 5, 6} | ||||
| B = {6, 7, 8} | ||||
|
