Set
A set is a collection of mathematical objects. Mathematical objects can range from points in space to shapes, numbers, symbols, variables, other sets, and more. Each object in a set is referred to as an element. Below are a few examples of different types of sets.
- A = {a, b, c, d, e} is a set made up of lower-case letters.
- B = {n|n ∈ N, 1 ≤ n ≤ 10} is a set made up of the first 10 natural numbers.
- C = {green, blue, red, yellow, white, black, purple} is a set made up of colors.
- M = {Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec} is a set made up of the 12 months in a year.
- P = the set of polygons shown in the figure below:
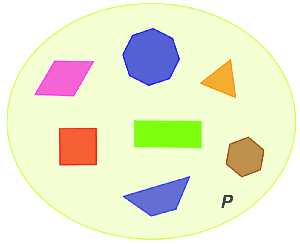
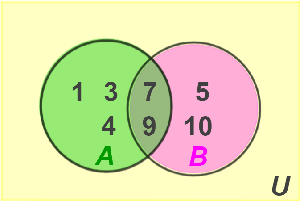
- 𝕌 = the universal set that contains subsets A and B, shown in the venn diagram below.
Ways to define a set
As can be seen in the list above, there are a number of different ways to define a set.
Definition through rules
A set can be defined using rules to determine the elements of the set. The rules must be strict such that the set is well-defined. For example, "the set of all even integers," is a well-defined set. There is nothing ambiguous about the set because the even integers are well-defined.
In contrast to the above, "the set of all young people who like ice cream," is not a well-defined set. "Young people" is an ambiguous term that doesn't specify age while the degrees to which people "like" ice cream cannot be quantified.
Roster notation
Roster notation defines a set using curly brackets to contain a list of the elements that make up the set, separated by commas. The set of all even integers can be defined in roster notation as:
A = {..., -6, -4, -2, 0, 2, 4, 6, ...}
Set-builder notation
Set-builder notation is similar to roster notation in its use of brackets, but rather than listing elements, conditions expressed using specific symbols (described in the table below) are applied to a larger set in order to specify a smaller set. For example, the set of all even integers is a subset of the set of all integers, and can be expressed in set-builder notation as
A = {2a | a∈ℤ}
where a is an integer, and "|" is read as "such that."
Set-builder notation can also be expressed in other ways. For example, the set of all integers greater than 12 could be expressed as:
B = {b∈ℤ | b>12}
Symbols used in set theory
There are many different symbols that are used within set theory. The table below includes some of the most common symbols.
| Symbol | Definition/meaning | Example |
|---|---|---|
| { } | Indicates a collection of elements | {1, 3, 7, 9} |
| ∅ | Empty set - set contains no elements/td> | {} |
| ... | Indicates that the set continues the pattern in the corresponding direction (towards negative (left) or positive (right) infinity) | {..., -9, -7, -3, -1, 1, 3, 7, 9, ...} |
| | | "Such that" | a∈ℤ | a > 3 - "a is an integer such that a is greater than 3" |
| ∩ | "and" or "intersection" | A = {1, 2, 3, 4} B = {4, 5, 6} A ∩ B = {4} |
| ∪ | "or" or "union" | A = {1, 2, 3, 4} B = {4, 5, 6} A ∪ B = {1, 2, 3, 4, 5, 6} |
| ⊆ | Subset - A is a subset of B if all its elements are included in B | {1, 2} ⊆ {1, 2, 3, 4, 5} {1, 2, 3, 4, 5} ⊆ {1, 2, 3, 4, 5} |
| ⊂ | Proper/strict subset - A is a proper subset of B if A is a subset of B, but not equal to B | {1} ⊂ {1, 2, 3, 4, 5} {1, 2} ⊂ {1, 2, 3, 4, 5} {1, 2, 3} ⊂ {1, 2, 3, 4, 5} {1, 2, 3, 4} ⊂ {1, 2, 3, 4, 5} |
| ∈ | Element of - indicates that the object on the left of the symbol is an element of the object on the right | x∈ℚ - "x is an element of the rational numbers" |
| 𝕌 | Universal set - the set of all possible values | A = {1, 2} B = {3, 4, 5} 𝕌 = {1, 2, 3, 4, 5} |
| Ac or A' | Complement - all the elements not in set A | 𝕌 = {1, 2, 3, 4, 5} A = {1, 2, 3} Ac = {4,5} |
| [a, b] | Closed interval - values between a and b including a and b | [1,4] = {1, 2, 3, 4} if only including integers |
| (a, b) | Open interval - values between a and b not including a and b | (1,4) = {2, 3} if only including integers |
| |A| | Order/cardinality - number of elements in the set | A = {3, 6, 7, 9} |A| = 4 |
| ℕ | Natural numbers - only positive numbers with no decimals or fractions | {1, 2, 3, ...} |
| ℤ | Integers - all positive and negative numbers with no decimals or fractions, including 0 | {..., -3, -2, -1, 0, 1, 2, 3, ...} |
| ℚ | Rational numbers - a number that can be represented as a fraction comprised of integers | ⅔ |
| ℝ | Real numbers - rational numbers and irrational numbers | π, e, 3, ½, 0.25 |
| ℂ | Complex numbers - numbers made up of a real and imaginary component | 4 + 2ⅈ |
