Mutually exclusive events
Mutually exclusive (or disjoint) events are events that cannot occur at the same time. Below are a few examples.
- A - Sue is 10 years old; B - Sue is 14 years old. Sue cannot be both 10 and 14 years old at the same time, so A and B are mutually exclusive events.
- A - Aaron scores an 85 on his statistics final; B - Aaron scores a 95 on his statistics final. Aaron cannot score an 85 and a 95 at the same time, so A and B are mutually exclusive events.
- A - rolling a die results in an odd number; B - rolling a die results in an even number. It is not possible to roll an odd and even number at the same time, so A and B are mutually exclusive.
Mutually exclusive events can be defined more precisely using set notation. Events A and B are mutually exclusive if they share no common outcomes:
A ∩ B = ∅
Probability of mutually exclusive events
By definition, mutually exclusive events share no common outcomes. Thus, the probability of A and B occurring is 0, or:
P(A ∩ B) = 0
In contrast, the probability of A or B occurring is a non-zero probability that can be calculated as the sum of the probabilities of A and B occurring:
P(A ∪ B) = P(A) + P(B)
For example, the probability of selecting an ace out of a standard 52-card deck is P(A) = 4/52 = 1/13. The probability of selecting a king is: P(B) = 1/13. If only one card is selected from the deck, P(A ∩ B) = 0 because it is not possible to select both a king and an ace on a single draw. Thus, A and B are mutually exclusive events.
On the other hand, if we wanted to know the probability of selecting an ace or a king, P(A ∪ B), we would simply sum their individual probabilities:
P(A ∩ B) = P(A) + P(B)
1/13 + 1/13 = 2/13
Venn diagrams
Mutually exclusive events can be depicted using Venn diagrams.
Example
Let the Venn diagram below represent the sample space S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and the events A, B, and C such that:
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8, 9}
C = {9, 10}
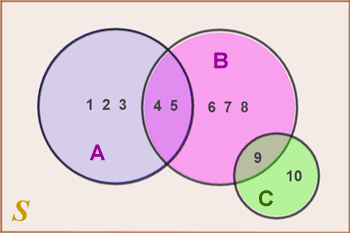
- Determine which (if any) events are mutually exclusive.
- Determine P(A ∩ C).
- Determine P(A ∪ C).
i. A and C are mutually exclusive because they have no shared outcomes. In other words: A ∩ C = ∅.
ii. Because A and C are mutually exclusive, P(A ∩ C) = 0.
iii. P(A ∪ C) = P(A) + P(C). There are 5 elements in A, 2 elements in C, and a total of 10 elements in the sample space. Thus:
P(A) + P(C) = 5/10 + 2/10 = 7/10
