Vector

Vectors, specifically Euclidean vectors, are mathematical objects that encode magnitude and direction. Vectors are ubiquitous in physics and describe quantities such as force, velocity, electric field, etc.

There are 2 common ways to think of vectors: geometrically and numerically. In the geometric mindset, vectors are thought of as arrows pointing in a certain direction with a certain length, or magnitude:

To describe a vector numerically, we first pick a coordinate system whose origin is at the start of the arrow. Then we associate the vector with the coordinates of its terminal end, which is indicated by the arrowhead:

Vectors are commonly written in the form of a column vector, where each value in the vector represents a component of the vector. Referencing the above vector, the x component has a value of 5, and the y component has a value of 7. Vectors are also commonly indicated with an arrow symbol above a letter. Referencing the above vector as vector v, we can therefore represent v as:

We can also have vectors in three dimensions or more:

We would write v as:

or as v = [4, 6, 8]^T. The "T" exponent stands for "transpose" and means to take the row vector, [4, 6, 8], and flip or transpose it into a column vector such that the leftmost entry becomes the top, and the rightmost becomes the bottom. The dimension of a vector is the number of coordinates it has. In the example above, since v has 3 coordinates, 4, 6, and 8, we say that v is 3-dimensional. Below, v, is 4-dimensional, w is 5-dimensional, and x is 6-dimensional:

Vector operations

Like scalars, there are a number of operations that we can apply to vectors. Below are some commonly used vector operations.

Vector addition

To add vectors, the vectors must be the same dimension. It is not possible to add vectors of different dimensions. For example, we can add [1, 3]^T + [3, 7]^T, but not vectors [1, 3]^T + [3, 7, 8]^T. Given that the vectors being added are the same dimension, simply add the components of the vectors to find their sum:

The order in which the vectors are added does not matter. Given two vectors, v and w, v + w = w + v. Geometrically, this is represented by starting from origin O, shifting by vector v to arrive at point S, then shifting by vector w to arrive at point P. Then, v + w is the vector from O to P. Similarly, we could also first shift by W to arrive at T, then shift by v to arrive at the same endpoint P. Thus, v + w = w + v in the geometric definition as well, as depicted in the figure below.

Given two vectors, v and w, where i represents the corresponding component of the vectors, vector addition can be represented in general form as:

Vector multiplication by scalars

To multiply a vector v by a scalar c, multiply each component of the vector by the scalar:

Geometrically, the vector cv lies on the same line as v except that it is scaled by a factor of c, which is why c is called a scalar. If |c| > 1, cv will be larger, or have a larger magnitude, than v. If c > 0, cv will point in the same direction as v. If c < 0, cv will point in the opposite direction as v. The diagram shows v being multiplied by -1 and 2:

Vector subtraction

Like vector addition, it is only possible to subtract vectors of the same dimension. Given two vectors v and w, v - w is computed by subtracting the coordinates of w from the corresponding coordinates of v:

v - w should be a vector that satisfies w + (v - w) = v. Therefore, using our knowledge of vector addition, the following diagram gives a geometric interpretation of v - w as the vector from the head of w to the head of v.

Another way to view vector subtraction is as addition in which the subtrahend is scaled by a factor of -1. In other words, v - w = v + (-1)*w.

Dot product

The dot product of two vectors is an algebraic operation that returns a scalar. It is the sum of the products of the corresponding components of the two vectors. Given two vectors, v = [v₁, v₂] and w = [w₁, w₂], the dot product, represented by a "·" is:

It is also worth noting that the dot product of a vector with itself is its magnitude squared:

The dot product is similarly computed for vectors of n dimensions - as the sum of the products of each corresponding component of the vectors. Another way to compute the dot product involves using the magnitudes of the vectors and the angle formed between them. If v = [v₁, v₂]^T, w = [w₁, w₂]^T, and θ is the angle between them, then their dot product can be found using the following formula:

It is worth noting that if the dot product of two vectors is 0, then the vectors are perpendicular. For example, the dot product of u = [2, 4]^T and v = [8, -4]^T is:

Vectors u and v are shown in the figure below:

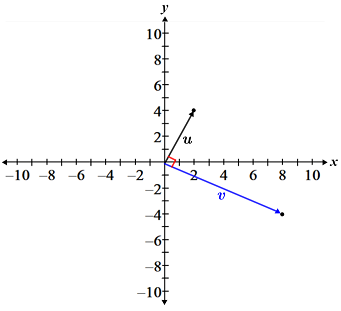
Cross product

The cross product of two vectors u and v produces a resultant vector, w, that is orthogonal to both of the vectors. Geometrically, this means that w lies in a different plane than both u and v, as shown in the figure below.

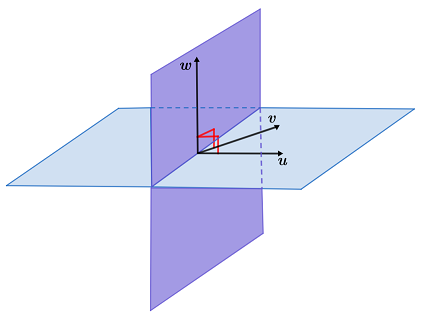
One method for computing the cross product of two vectors involves using their components. Let u = [u₁, u₂, u₃] and v = [v₁, v₂, v₃]. Then, the resultant vector w can be computed using the following formula,

Thus:

Another method for finding the cross product of two vectors uses the sine of the angle between the two vectors. The cross product of two vectors u and v with angle θ between them is,

where is a unit vector that is orthogonal to the plane containing u and v. This can be represented geometrically using a parallelogram formed by the cross products:

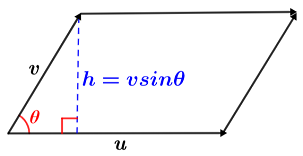
Vectors u and v are translated to form the parallelogram shown above. The height of the parallelogram, h, can be found using right angle trigonometry and the sine function. Since the area of the parallelogram is A = bh,

Thus, the cross product can be computed as:

We do not need to include in the formula because it has unit length.