Composite number
A composite number is a positive integer with more than two factors. This means that it can be formed by the product of whole numbers other than 1 and itself. 4 is the smallest composite number:
2 × 2 = 4
It can be formed by multiplying two whole numbers, 2 and 2, so it is the first number that meets the definition of a composite number, with 6 (2 × 3) being the next one.
Composite numbers are the counterpart of prime numbers. All positive integers greater than 1 are either composite or prime numbers. Both 1 and 0 are neither composite nor prime numbers. Below is an example of one way to represent composite numbers using arrays.
Example
16 is a composite number. Its factors are 1, 2, 4, 8, and 16. We can form 16 in a number of ways, as shown using the arrays of squares in the figure below.
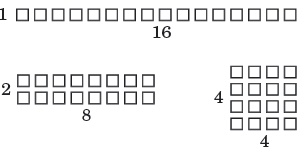
The above arrays are equivalent to:
16 = 1 × 16
16 = 2 × 8
16 = 4 × 4
Fundamental theorem of arithmetic
The fundamental theorem of arithmetic states that any integer greater than 1 is either prime, or can be represented using a unique product of prime numbers. As an example, 36 is a composite number that can be formed by multiplying 12 and 3 (as well as other factors). 12 can be further broken down into 4 × 3, and 4 can again be broken down into 2 × 2. Therefore, 36 can be represented as a product of the following prime numbers:
36 = 3 × 3 × 2 × 2
No matter how we arrange this set of prime numbers, or whatever order we multiply them in, two 3s and two 2s can only form 36. According to the fundamental theorem of arithmetic, this holds true for any non-prime number greater than 1. This is one of the reasons that prime numbers are extensively studied. They can be thought of as the building blocks of all numbers, since all positive integers greater than 1 are either prime, or composite numbers that can be formed by multiplying prime numbers.
