Cross product
The cross product is a binary operation, involving two vectors, that results in a third vector that is orthogonal to both vectors. The figure below shows two vectors, u and v, and their cross product w.
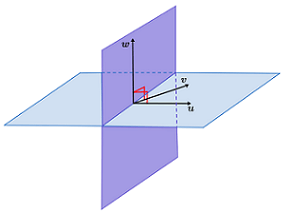
Notice that u and v share the same plane, while their cross product lies in an orthogonal plane. This will always be the case since the resultant vector of the cross product must be orthogonal to both vectors.
How to compute the cross product
There are a number of different ways to compute the cross product. Note that the dot product and cross product are not the same. The result of the dot product is a scalar, while the result of the cross product is a vector. Note that the cross product is essentially the determinant of a 3 × 3 matrix, so one way to compute the cross product is to write the vectors in the form of a 3 × 3 matrix with the standard basis vectors, i, j, and k as the first row of the matrix such that:
The cross product, w, can then be computed as:
Example
Find w, the resultant vector for u × v, where u = [-2 3 4] and v = [1 5 6].
Geometric interpretation of the cross product
The cross product can also be computed as:
where θ is the angle between vectors u and v, and n is the unit vector that indicates the direction of the cross product (which can be determined using the right-hand rule). Refer to the figure below:
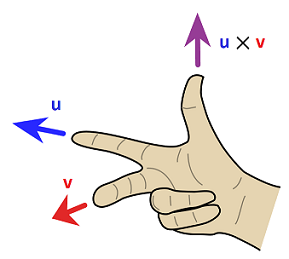
By placing the index finger, middle finger, and thumb in the orientation shown in the figure, with the index finger along vector u and middle finger along vector v, the thumb will point in the direction of the resultant vector of the cross product.
The magnitude of the cross product is computed as:
In the figure below, vectors u and v are used to form a parallelogram.
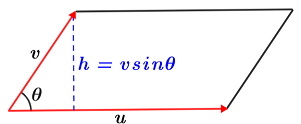
The base of the parallelogram has length u, while the height is indicated by h, which can be computed as v sin(θ). Since the area of a parallelogram is the product of its base and height, the area of the parallelogram is equal to the magnitude of the cross product:
To find the angle θ given two vectors, we can use the formula above.
Example
Find θ for vectors u = [-2 3 4] and v = [1 5 6].
First find ||u|| and ||v||:
From the previous example above, u × v = [-2 16 -13], so:
Plugging these into the formula for the magnitude of the cross product and solving for θ yields:
Thus, the angle between vectors u and v is 29.24°.
Consider the following example, which leads us to an interesting fact about the standard unit vectors in the 3D coordinate system.
Example
Find the unit vector orthogonal to u = [4 3 0] and v = [-4 5 0].
The cross product of vectors u and v produces an orthogonal vector:
Then, to find the unit vector, normalize the cross product by dividing by its magnitude:
The orthogonal unit vector is then:
Refer to the figure below:
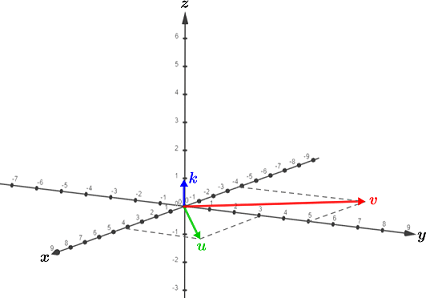
Notice from the graph above that vectors u and v lie in the xy-plane in the 3D coordinate system. The orthogonal unit vector [0 0 1] is the standard unit vector, k, which points in the same direction as the z-axis. The other two standard unit vectors are i = [1 0 0] and j = [0 1 0]. The cross product of any two of these standard unit vectors produces the third standard unit vector:
Similarly,
Scalar triple product
The scalar triple product is the dot product of one 3D vector with the cross product of two other 3D vectors, or,
where vector u = [u1 u2 u3], v = [v1 v2 v3], and w = [w1 w2 w3]. The triple scalar product can also be computed as the determinant of a 3 × 3 matrix such that:
To show how this works, first find v × w:
Then, take the dot product of u and v × w:
The 3 expressions in parentheses from the last step above are determinants for the matrix of minors for u1, u2, and u3. We can confirm that the triple scalar product is equal to the determinant of the 3 × 3 matrix by computing the determinant
which is the same result obtained above.
Example
Find the triple product given u = [1 2 3], v = [0 -1 4], and w = [-2 5 1].
