Eigenvector

A nonzero vector, x, is an eigenvector of some linear transformation if the linear transformation produces a scalar multiple of x,

where T is a linear transformation, and λ is referred to as an eigenvalue of the corresponding eigenvector x. In the context of matrices, an eigenvector is therefore a vector that, when multiplied by some transformation matrix, results in the eigenvector multiplied by some scalar; multiplying the vector by a matrix or a scalar therefore produces the same result:

where A is an n × n matrix, x is a non-zero vector, and λ is the corresponding eigenvalue. Geometrically, an eigenvector is a vector pointing in a given direction that is stretched by a factor corresponding to its eigenvalue. Consider the following figure.

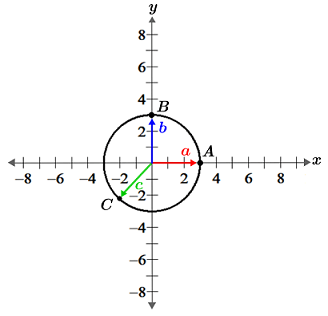
In the figure, A, B, and C are points on a circle whose positions are determined by vectors a, b, and c respectively. Given that a, b, and c are eigenvectors, a transformation that scales each vector by a factor of 2 will result in a circle with a radius that is double that of the original circle. The transformed vectors all point in the same direction as their original vectors; the only difference is that they are scaled by λ, the eigenvalue, which in this case is 2:

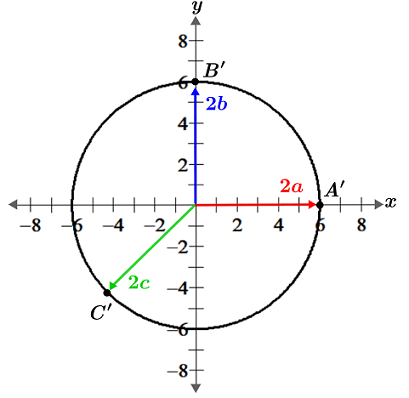
We can confirm this by computing the magnitudes of vectors c and 2c as an example, which can be represented in column vector form as follows:

Vector c has a magnitude of,

and 2c has a magnitude of:

The angle formed by vector c with the x-axis is,

and the angle formed by 2c with the x-axis is:

Thus, 2c is twice the magnitude of c, and both point in the same direction, confirming that 2 is the corresponding eigenvalue of eigenvector c. The same is true for each of the vectors shown in the figures above.

How to find an eigenvector

To find an eigenvector for a given square matrix, we need to first determine the eigenvalue, which we can do using the matrix definition of an eigenvector:

Set this equation equal to 0 (a zero matrix) such that:

We can then multiply λ by the corresponding n × n identity matrix I, which doesn't change the value of λ while also allowing us to combine it with matrix A such that:

Since x is an eigenvector, we know that it must have a non-zero value, or the solution to the above expression would be trivial. In cases where the matrix, (λI - A), is invertible, eigenvector x would equal 0; we want to find solutions such that this is not the case. Recall that if the determinant of a matrix is equal to 0, that the matrix is not invertible. Thus, we take the determinant of the above expression and set it equal to 0 in order to solve for the eigenvector of the system:

The above expression, det(A - λI) is referred to as the characteristic polynomial of A, and the entire equation is referred to as the characteristic equation. The eigenvalues of A can therefore also be referred to as characteristic values of A, where the eigenvalues of A are the roots of the characteristic polynomial such that:

After determining the eigenvalues of A, we can then substitute each eigenvalue into Ax = λx to find the corresponding eigenvectors.

Examples

Find the eigenvectors of the following systems.

1.

First, find the eigenvalues:

Then, find the determinant:

Thus, the characteristic polynomial is λ² - 5λ + 6, and setting this equal to 0 and solving for λ yields the eigenvalues of A:

Then, to find the corresponding eigenvectors, substitute each eigenvector into Ax = λx, where . When λ = 2:

Writing the above in the form of a system of equations yields:

The second equation is true for any real value of x₂, so let x₂ = s, where s is a non-zero real number. Substituting x₂ into the first equation yields x₁ = s, so

meaning that or any multiple of is an eigenvector that corresponds to the eigenvalue of 2. For example, if , then

When λ = 3:

Writing the above in the form of a system of equations yields:

In order to satisfy the second equation, x₂ must equal 0. Substituting this into the first equation yields 3x₁ = 3x₁, which is true for any real value of x₁. Let x₁ = s, where s is a non-zero real number. Then:

Thus, the eigenvector corresponding to the eigenvalue of 3 is any multiple of .

2.

First, find the eigenvalues:

Then, find the determinant:

Thus, the characteristic polynomial is -λ³ + 7λ² - 14λ + 8 and setting this equal to 0 and solving for λ yields the eigenvalues of A:

Then, to find the corresponding eigenvectors, substitute each eigenvector into Ax = λx, where . When λ = 1,

Writing the above in the form of a system of equations,

For the third equation to be true, x₃ must equal 0. Substituting this into the second equation,

,

so x₂ must also be 0, and the first equation becomes:

,

which is true for all real values of x₁. Let x₁ = s, where s is a non-zero real number. Then:

,

Thus, the eigenvector corresponding to the eigenvalue of 1 is .

For λ = 2:

In the form of a system of equations,

For the third equation to be true, x₃ must equal 0. Substituting this into the second equation yields 2x₂ = 2x₂, which is true for all real values of x₂. Let x₂ = s, where s is a non-zero real number. Substituting these values into the first equation yields:

Thus, x₁ = 2s, so:

Thus, the eigenvector corresponding to the eigenvalue of 2 is .

For λ = 4:

Writing the above in the form of a system of equations,

The third equation is true for all real values of x₃. Let x₃ where s is a non-zero real number. Substituting this into the second equation yields,

,

and .

Next, substitute x₂ and x₃ into the first equation to find x₁:

Thus, the eigenvector corresponding to an eigenvalue of 4 is .