Gradient
The gradient for a function of several variables is a vector-valued function whose components are partial derivatives of those variables. The gradient can be thought of as the direction of the function's greatest rate of increase.
Formally, given a multivariate function f with n variables and partial derivatives, the gradient of f, denoted ∇f, is the vector valued function,
where the symbol ∇, named nabla, is the partial derivative operator. For example, to find the gradient, ∇f(1, 2, 3) for f(x, y, z) = 4x2yz2 + 2xy2 - xyz, take the partial derivatives of x, y, and z:
Substituting 1, 2, and 3 in for x, y, and z then yields:
Properties of the gradient
Let y = f(x, y) be a function for which the partial derivatives fx and fy exist.
- If the gradient for f is zero for any point in the xy plane, then the directional derivative of the point for all unit vectors is also zero. That is, if ∇f(x, y) = 0, then Du(x, y) = 0 for any u.
- The directional derivative for any point in the xy plane has its maximum increase when it is in the direction of its gradient. Its maximum value is the magnitude of its gradient. That is, if ∇f(x, y) ≠ 0, then the maximum of Du(x, y) is ||∇f(x, y)||.
- The minimum value for the directional derivative at any point in the xy plane is -||∇f(x, y)|| in the direction of -∇f(x, y).
Geometric interpretation of the gradient for a function of two variables
Consider the following graph with gradient vectors denoted in red. The graph of z = f(x, y) is a paraboloid opening upward along the z-axis whose vertex is at the origin.
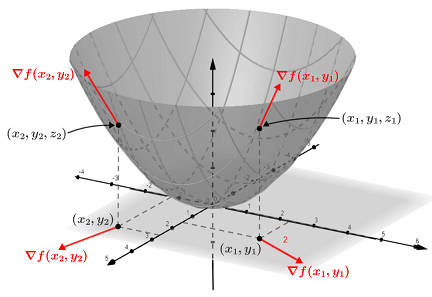
The gradient vectors ∇f(x1, y1) and ∇f(x2, y2) drawn in the xy-plane have their initial points placed at (x1, y1) and (x2, y2) respectively. Note that the gradient vectors are calculated in component form but are translated to their respective input points on the xy plane to better show the direction associated with those points. If we could fold the xy plane so each input (x, y) maps to their corresponding output value (x, y, z) on the paraboloid, then each corresponding gradient vector can also be mapped onto the paraboloid such that its initial point is at (x, y, z). The gradient vectors mapped to (x1, y1, z1) and (x2, y2, z2) show the direction of fastest increase.
Gradient vector field
Finding the gradient for each point in the xy plane in which a function f(x, y) is defined creates a set of gradient vectors called a gradient vector field. The gradient vector field gives a two-dimensional view of the direction of greatest increase for a three-dimensional figure. A gradient vector field for the paraboloid graphed above is shown below:
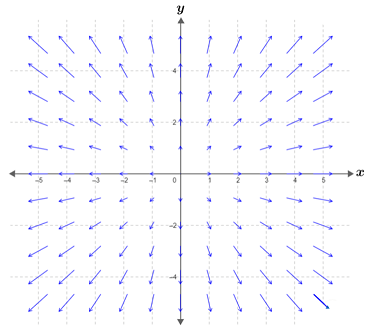
The equation of the paraboloid above is f(x, y) = 0.3x2 + 0.3y2. The equation of the vector field is:
Notice that the vectors lengthen as they move away from the origin, confirming that the surface of the paraboloid gets steeper the further from the origin it gets.
Using gradients to find directional derivatives
The directional derivative of a function z = f(x, y) in the direction of the unit vector , where the partial derivatives fx and fy exist, is:
If the direction is given as an angle θ in standard position, then , and
Example
Find the directional derivative for at (-2, 2) in the direction of
.
Since the direction is given as an angle, the unit vector is:
Computing the partial derivatives yields:
and
The directional derivative is then:
At (-2, 2),
The value of the directional derivative in the direction of the unit vector u (graphed in component form) can be thought of as the slope of the line on the surface of the curve of f in the direction of u at (-2, 2, 4), as indicated in red in the figure below:
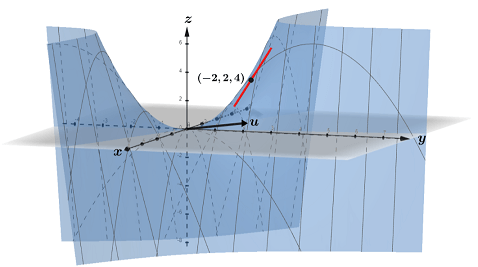
There are many directional derivatives that can be calculated at (-2, 2, 4) for f depending on the desired direction. The directional derivative with the largest magnitude can be found by using the gradient of f.
Also, since the gradient is a vector, we can use it to determine the directional derivative of a function in the direction of some unit vector. From the definition of a directional derivative above, the vector that is the partial derivative of x and y is the gradient of f:
Substituting the gradient into the formula for the directional derivative yields:
Example
Find the directional derivative of f(x,y) = x3e-y at (3, 2) in the direction of .
For this example, the direction is given as a vector, but not a unit vector. To find the unit vector, divide vector v by its magnitude:
We then compute the gradient as follows:
At (3, 2), . Thus:
Du(3, 2) = -0.73 can be thought of as the slope of the line on the surface of f at (3, 2, 3.65) in the direction of v, as shown in red in the figure below:
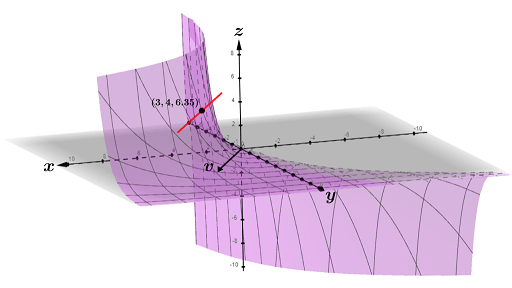
The line with the steepest slope on the surface of the graph of f at (3, 2, 3.65) lies on the gradient vector w at the point (3, 2) in the xy plane:
The graph of w in the xy plane and its projection onto the surface of f at (3, 2, 3.65) is shown in the figure below:
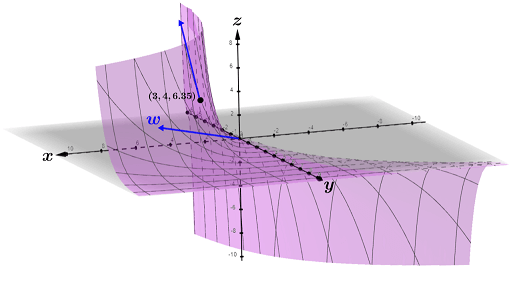
Also, for a function z = f(x, y), the magnitude of the gradient in the xy plane is the maximum value of the directional derivative at that point that is in the same direction as its corresponding gradient.
The magnitude for gradient vector w is
so the maximum value of any directional derivative for f at (3, 2, 3.65) is 5.17 and points in the same direction as w.
