Partial derivative

A partial derivative is the derivative with respect to one variable of a multi-variable function. For example, consider the function f(x, y) = sin(xy). When analyzing the effect of one of the variables of a multivariable function, it is often useful to mentally fix the other variables by treating them as constants. If we want to measure the relative change of f with respect to x at a point (x, y), we can take the derivative only with respect to x while treating y as a constant to get:

This new function which we have denoted as is called the partial derivative of f with respect to x. Similarly, if we fix x and vary y we get the partial derivative of f with respect to y:

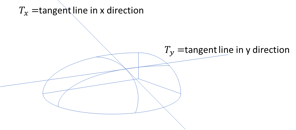
Note: When denoting partial derivatives, f_x is sometimes used instead of . Geometrically, and represent the slopes of the tangent lines of the graph of f at point (x, y) in the direction of the x and y axis respectively.

Formal definition

The formal definition of the partial derivative of the n-variable function f(x₁ ... x_n) with respect to x_i is:

Note: the phrase "i^th partial derivative" means .

The partial derivatives of f(x₁...x_n) such as are themselves functions of x₁,..., x_n. Therefore we can just as easily take partial derivatives of partial derivatives and so on. For example, the x-partial derivative of , denoted , is -y²sin(xy). Similarly:

Notice that . It turns out that this process of exchanging the order of variables with respect to which we take partial derivatives yields the same answer for any function. This fact is known as the equality of mixed partials.

Theorem: equality of mixed partials

Note: When writing higher order partial derivatives, we normally use and in place of and respectively.

Directional derivative

The partial derivatives represent how the function f(x₁, ..., x_n) changes in the direction of each coordinate axis. But how do we measure the relative change in f along an arbitrary direction that doesn't align with any coordinate axes? Let's say you are starting at a point p = (p₁, ..., p_n) and you want to find the relative change or "slope" in f caused by an infinitesimal change along a unit vector . Then the directional derivative of D_uf of f in direction u at p is given by:

where the p subscript means that we are taking partial derivatives at p. To understand why this measures the relative change along unit vector u, start with a function of a single variable. In that case, there is only one direction and so the directional derivative in that direction is as we expect. In two variables, recall the image

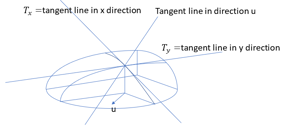
and notice that the tangent lines make a plane that is also tangent to the curve at point p = (x₀, y₀). The equation of the plane is:

where Δx = x - x₀ and Δy = y - y₀ represent the change in x and y away from (x₀, y₀). When (x, y) = (x₀, y₀), the z-value should just be f(x₀, y₀). For every unit step in the positive x direction, the z-value should increase by units. Similarly, the z value should increase by units for every unit step in the positive y direction. If we define the change in z as Δz = z - f(x₀, y₀), then the change in the direction of vector u = [Δx, Δy]^T is . We can generalize this to a change in f(x₁,..., x_n) in the direction u = [Δu₁,...,Δu_n]^T to get . If we require u to be a unit vector, then this expression is our original definition of a directional derivative.

Gradient

At a point p, the gradient, ∇f_p, of f(x₁, ..., x_n) is defined as the vector:

We can express the directional derivative at p in the direction of unit vector u as the dot product,

One property of the dot product is that , where ||v|| denotes the magnitude or Euclidean norm, , and θ is the angle between v and w when both their tails are at the same point. Therefore,

but ||u|| = 1, since u is a unit vector, so

The directional derivative is maximized when cos(θ) = 1 or θ = 0 and minimized when cos(θ) = -1 or θ = π. When θ = 0, u points in the same direction as ∇f_p, and when θ = π, u points in the opposite direction as ∇f_p. In summary, the directional derivative is maximized when u points in the same direction as ∇f_p and minimized when u points in the opposite direction of ∇f_p. Remembering that the directional derivative measures relative change, we have proven the following theorem: The gradient always points in the direction of steepest increase.

Multivariable chain rule

Suppose that each of the n variables of f(x₁,..., x_n) is also a function of m other variables, w₁,..., w_m, so each x_i can be written as x_i(w₁,..., w_m). Then we have the following diagram of dependencies where each arrow means that the variable at the tail of the arrow controls the variable at the head of the arrow.

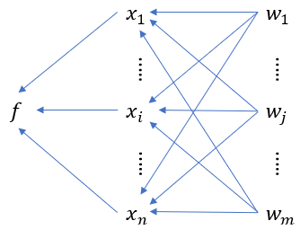
If we want to take the partial derivative , we should look at all the possible paths from w_j to f, which represent all the ways in which w_j indirectly influences f. For a given path, say w_j → x_i → f, a change Δw_j in w_j produces a change in x_i which is magnified by a factor of . This change in x_i in turn produces a change in f which is magnified by a factor of . For this path, a change in w_j gets magnified by a net factor of to produce a change in f.

Then we add up the changes from all the possible combinations of paths to get the total change in f:

Dividing by Δw_j gives you the change in f relative to the change in w_j, the limit of which is the partial derivative :

Because we found by adding up all the changes in f caused by a change in w_j, is sometimes called the total derivative of f with respect to w_j.