First derivative test
The first derivative test is used to examine where a function is increasing or decreasing on its domain and to identify its local maxima and minima.
The first derivative is the slope of the line tangent to the graph of a function at a given point. It may be helpful to think of the first derivative as the slope of the function. When the slope is positive, the graph is increasing. When it is negative, the graph is decreasing. Points at which the slope is 0 are referred to as critical points, and are points that might be local minima or maxima. The first derivative test involves testing the behavior of the function around these points to determine whether or not they are local minima or maxima.
The first derivative test is based on the fact that the sign of the first derivative does not change between critical points. Thus, if we find the critical points of a function, we can test points within the intervals between critical points to determine whether the function is increasing or decreasing over those intervals. Then, by determining whether the function is increasing or decreasing before and after a critical point, we can identify whether the point is a minimum, maximum, or neither.
First derivative test for maxima and minima
Given a differentiable function, the first derivative test can be used to find the local minima or maxima of the function through the following steps:
- Find f'(x).
- Solve for f'(x) = 0 or undefined to find the critical points of the function.
- Test a point within each interval between critical points to determine whether the function is increasing or decreasing within the interval; a function is increasing at a point a if f'(a) > 0; it is decreasing at a if f'(a) < 0.
After finding the critical point(s) of the function, we can apply the first derivative test. Let a be a critical point such that f'(a) = 0.
- If f' changes from positive to negative at x = a, then f has a local maximum at a.
- If f' changes from negative to positive at x = a, then the point is a local minimum at a.
- If f' does not change sign at x = a, then f does not have a local extrema at a.
Example
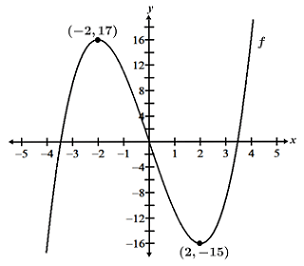
Find any relative extrema for f(x) = x3 - 12x + 1.
First, differentiate the function:
Then, solve for f'(x) = 0 or undefined. In this case, since f(x) is a polynomial, it is defined over its entire domain, and we only need to solve for f'(x) = 0.
Thus, x = -2 or 2. These are the critical points of f(x), and the intervals we need to test are therefore (-∞, -2), (-2, 2), and (2, ∞). Recall that within these intervals, the sign of f' does not change, so we only need to select one point within each interval. Plugging x = -3, 0, and 3 into f',
we find that f' is positive over the interval (-∞, -2), negative over the interval (-2, 2), and positive over the interval (2, ∞), which means that the graph of f(x) is increasing, decreasing, and increasing over these respective intervals, as shown in the table below:
| Interval | Sign of f' | f is increasing/decreasing |
|---|---|---|
| (-∞, -2) | + | increasing |
| (-2, 2) | - | decreasing |
| (2, ∞) | + | increasing |
Using this table, we can then determine whether f(x) has local extrema at these critical points. Since the sign of f' changes from positive to negative at x = -2, f has a maximum at x = -2; since the sign of f' changes from positive to negative at x = 2, f has a minimum at x = 2, which we can confirm in the graph below: