Second derivative test

The second derivative test is used to determine whether a critical point of a function is a local minimum or maximum using both the concavity of the function as well as its first derivative. Recall that the derivative of a function represents the rate of change of the function. The first derivative f'(x) is the rate of change of f(x), or its slope, while the second derivative f''(x) represents the rate of change of f'(x), and also the concavity of f(x).

Local extrema occur at points on the function at which its derivative is not changing, or f'(x) = 0; these points are referred to as critical points. This makes sense if we consider what local maxima and minima are. For a function to have a local maximum at some point within an interval, all surrounding points within the interval must be lower than the point of interest. Similarly, for a function to have a local minimum at some point within an interval, all surrounding points must be higher. Thus, maxima and minima can only occur at points where the slope of the function is neither increasing nor decreasing. Otherwise, the point cannot be a maximum or minimum because the surrounding points will be higher and lower than the point of interest.

While the first derivative helps us determine the points at which a function may have a local extremum, the second derivative tells us the concavity at said points:

The concavity at a given point can then be used to determine whether the point is a local maximum, minimum, or something else. Consider the following figure:


Concave up Concave down

As can be seen from the figure, if f(x) is concave up over an interval, it has a local minimum within that interval; if f(x) is concave down over an interval, it has a local maximum within that interval. Using the first derivative to find critical points, then using the second derivative to determine the concavity at those points is the basis of the second derivative test.

Second derivative test:

Let f(x) be a function such that both f'(x) and f''(x) exist. For all critical points, f'(x) = 0,

Example

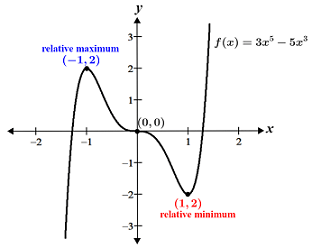
Find any relative extrema for f(x) = 3x5 - 5x3.

First, find the critical points by solving for f'(x) = 0:


Setting each factor equal to 0 and solving for x, we find that x = -1, 1, or 0. These are the critical points of f(x), and where the function may have a minimum or maximum.

Next, find the second derivative of f(x) and determine the value of f''(x) for each critical point:



Thus, according to the second derivative test, f(x) has a maximum at x = -1 and a minimum at x = 1. At x = 0, the result of the second derivative test is inconclusive. To determine whether x = 0 is an inflection point, test the concavity of f(x) before and after the inflection point by selecting a test point in the appropriate interval. Since the critical points are -1, 0, and 1, the intervals that we need to test are (-1, 0) and (0, 1). Within these intervals, the concavity does not change, so we only need to test one value within each interval. Selecting x = -0.5 and 0.5, the concavity in the respective intervals are:



Thus, f(x) is concave up over the interval (-1, 0) and concave down over the interval (0, 1). Since the concavity changes at x = 0 from concave up to concave down, x = 0 is an inflection point. Note that whether f''(x) changes from positive to negative or vice versa does not matter; as long as the sign changes, the critical point is an inflection point. Below is a graph of f(x):