Point slope form
Point-slope form is one of the more commonly used forms of a linear equation, and has the following structure:
y - y1 = m(x - x1),
where m is the slope of the line, (x1, y1) is a point on the line, and x and y are variables representing other points on the line. Point-slope form can be used when one point on the line and the slope are known. It is useful for finding other points on a line given that at least one point and the slope of the line are known.
Notice that point-slope form is more or less a rearranged form of the slope formula, y = mx + b:
The reason we use x and y instead of x2 and y2 is that in the slope formula, we were solving for m by using two points, but when we are using point-slope form, we are writing a linear equation, so x and y need to be there in the final equation as variables rather than as known points.
Given two points, you can write an equation in point-slope form:
| (x, y) | (x1, y1) |
| (-5, 3) | (3, 7) |
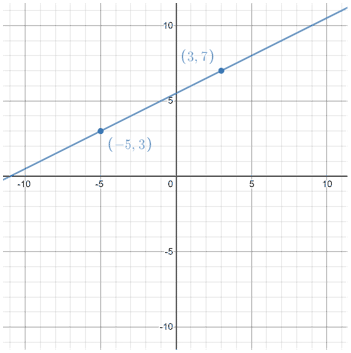
Note that in the example above, we can write the equation in point-slope form using either of the two known points. We need both points in order to calculate the slope, but only one of the points to write the linear equation. In the example above, we used the point (3, 7) to write the linear equation, but we also could have used (-5, 3), in which case the equation of the line would be expressed as:
Both equations represent the same line, and when writing an equation in point-slope form, the decision of which point to use is entirely up to you.
Other forms of linear equations
Point-slope form is just one of a number of different forms of a linear equation, all of which have different uses depending on the context. As mentioned above, point-slope form is most useful when one point on a line as well as the slope of the line are known. In such cases, point-slope form makes it easy to come up with an equation of a line and graph it. One of the drawbacks of point-slope form is that it cannot be used to represent the equation of a vertical line, since vertical lines have undefined slopes.
Other commonly used forms include slope-intercept form and standard form.
Slope-intercept form
Slope-intercept form is the most commonly used form for the equation of a line, and is expressed as
y = mx + b
where m is the slope, and b is the y-intercept. It is similar to point-slope form except that it involves the slope of a line and its y-intercept, rather than the slope of a line and a point on the line. It is the special case of point-slope form given that the point on the line is also the y-intercept. It is useful because given a slope and y-intercept, it is easy to write the equation of a line in slope-intercept form, as well as graph it. Often, the equation of a line in other forms is converted to slope-intercept form because of how convenient it is to work with.
Like point-slope form, one of the disadvantages of slope-intercept form is that vertical lines cannot be represented in slope-intercept form since the slope of a vertical line is undefined.
Standard form
The standard form for the equation of a line is expressed as
Ax + By = C
where A, B, and C are usually integers. Standard form is useful for solving systems of linear equations. Unlike point-slope and slope-intercept form, standard form can be used to represent the equation of a vertical line, since it does not involve the use of the slope of the line.
There are other forms used to represent linear equations as well, but these are a few of the most commonly used in algebra.
