Standard form
Standard form is a term commonly used to describe the most typical form of an object (like a number, expression, equation, etc.) used in a number of different topics. In this case, standard form refers to the standard form of a linear equation. The standard form of a linear equation is given by the equation:
Ax + By = C
where A, B, and C are constants.
Standard form is useful because the x- and y-intercepts of the line can be easily found by setting x or y equal to 0, then solving for the desired variable. Doing so results in the general formulas for finding the x and y-intercept given a linear equation in standard form:
One of the key benefits of the standard form of a linear equation over point-slope form and slope-intercept form is the ease with which it can be used to find the x-intercept. Finding the x-intercept using either of these two other forms is more tedious than it is with standard form.
Once the x and y-intercepts are found, the line can be graphed by plotting the x and y-intercepts then drawing a line connecting the intercepts.
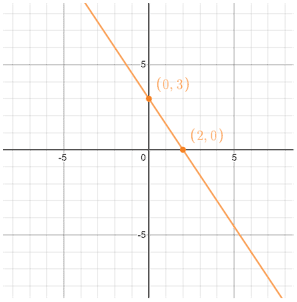
Example:
3x + 2y = 6
| 3x + 2(0) = 6 | 3(0) + 2y = 6 |
| 3x = 6 | 2y = 6 |
| x = 2 | y = 3 |
| x-intercept at (2, 0) | y-intercept at (0, 3) |
Depending on the linear equation, it can be easier to graph a line given an equation in slope-intercept or point-slope form, since it can be tedious to calculate the x and y-intercepts given an equation in standard form. Equations in slope-intercept and point-slope form include the slope of the line, and a point on the line, which can be immediately read from the equation. Thus, plotting the line doesn't require any calculation of the intercepts.
Converting to standard form
Different forms of linear equations are useful for different applications. For example, when solving systems of linear equations, it is helpful to first convert the equation into standard form. Slope-intercept and point-slope form are two commonly used forms of a linear equation that, while useful for graphing, are not useful for solving systems of linear equations. It is therefore important to know how to convert between various forms of linear equations to best suit the application.
Converting from point-slope or slope-intercept form to standard form involves moving all the variables to one side of the equation, moving the constant to the other side, then manipulating the equation as necessary such that the coefficients of the terms of the equation are integers.
Examples
Convert the following linear equations to standard form.
1. y = -3/4x + 2:
3/4x + y = 2
3x + 4y = 8
2. y - 2 = 3/4(x - 8):
y - 2 = 3/4x - 6
-3/4x + y = 4
-3x + 4y = 16
Other forms of a linear equation also exist, but the above are a few of the most common.
