Slope

Slope is a value that describes the steepness and direction of a line. The slope formula is as follows:

Rise over run

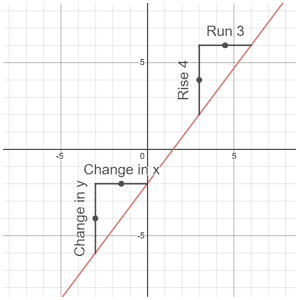
Slope is commonly represented by the lower-case letter "m," and is often referred to as rise over run. The formula essentially calculates the change in y over the change in x using two points (x₁, y₁) and (x₂, y₂). A graphical depiction is shown below.

Below is an example of using the slope formula.

As the magnitude of the slope increases, the line becomes steeper. As the magnitude of the slope decreases, the opposite occurs, and the line becomes less steep.

For linear equations in slope-intercept form, y = mx + b, m indicates the slope of the line.

Positive slope

Slope also indicates the direction of a line. A line with a positive slope, said to be increasing, runs upwards from left to right.

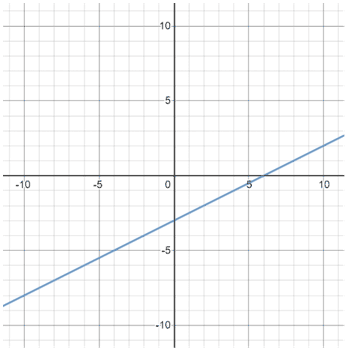
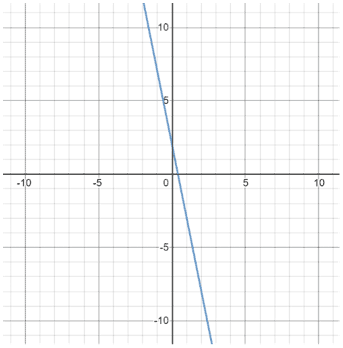
Negative slope

A line with a negative slope, said to be decreasing, runs downwards from left to right.

Horizontal line slope

A horizontal line has a slope of zero because y does not change:

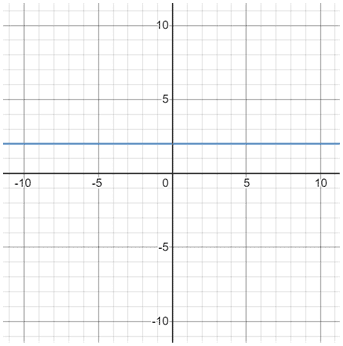
Vertical line slope

A vertical line has an undefined slope because you cannot divide by zero (x does not change).

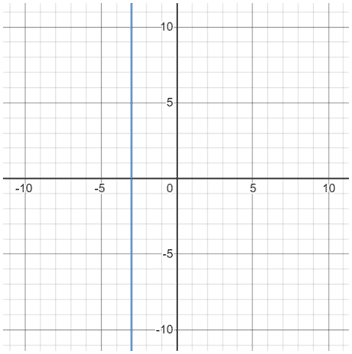
Parallel line slope

y = 2x + 3 and y = 2x - 4 both have a slope of 2, so they are parallel, as shown below:

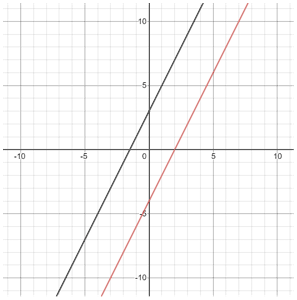
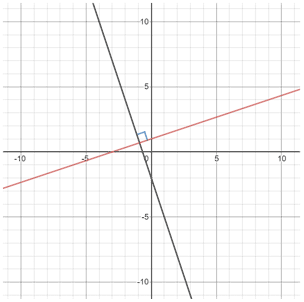
Perpendicular line slope

Perpendicular lines have slopes that are "opposite reciprocals" of each other. In this context, "opposite" refers to the change in sign from + to - or vice versa. "Reciprocal" refers to flipping the numerator and denominator of the value. For example, the reciprocal of x is .

Therefore, taking the opposite reciprocal of something means that you flip the sign and the numerator and denominator.

-3x - 2 has a slope of -3, and y = ⅓x + 1 has a slope of ⅓. -3 and ⅓ are opposite reciprocals, so the equations are perpendicular: