Linear equations
A linear equation is an equation that represents a straight line. When plotted on a graph, a linear equation always results in a straight line, as in the figure below, which is a special case of a linear equation referred to as the identity function, y = x:
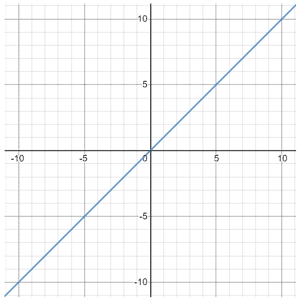
It is referred to as the identity function because inputting any x-value will return the same value of y.
In most cases, the term "linear equation" refers to one-variable linear equations (like the one above), though linear equations can have more variables, as long as all of the variables are first-order variables. A first-order variable, also referred to as a variable of degree 1, refers to the exponent on the variable. For example, the equation below is not a linear equation. The degree of each term is included for reference, though by convention, usually only exponents that are not 0 or 1 are shown:
y1 = 2x3 - 3x1 + 40
The degree of a polynomial is determined by the highest order term in the polynomial. In this equation, the highest degree is 3, making the equation non-linear. All variables involved must be of degree 1 for the equation to be linear.
Any number of constants can be present (since their degree is 0). If an equation only has a constant, the equation is a horizontal (ex. y = 4) or vertical line (ex. x = -2).
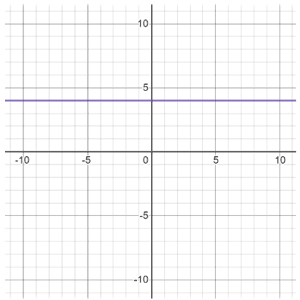
|
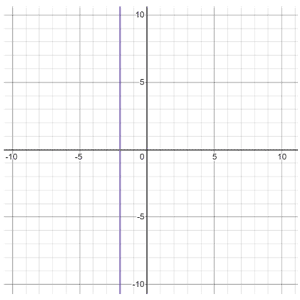
|
Forms of linear equations
Linear equations can take on multiple forms including slope-intercept form, point-slope form, standard form, and more.
Slope-intercept form
Slope-intercept form is probably the most commonly used form of a linear equation. It is typically expressed as
y = mx + b
where m is the slope, and b is the y-intercept.
The equation of a line can be written in slope-intercept form when the slope and y-intercept of the line are known. Or, given an equation in slope-intercept form, it is easy to quickly identify the slope and y-intercept of the line. Graphing the equation of a line is also relatively simple when given an equation in slope-intercept form.
Point-slope form
Point-slope form is similar to slope-intercept form except that it is based on some point on the line, rather than the y-intercept specifically. It is typically expressed as
y - y1 = m(x - x1)
where (x1, y1) represent a point on the line, and m is the slope. Like slope-intercept form, it is also useful for graphing, and has the benefit of being usable using any point on the line rather than just the y-intercept specifically, as is the case with slope-intercept form.
Standard form
The standard form for the equation of a line is typically expressed as
Ax + By = C
Where A, B, and C are integers, and A and B are not equal to 0. One of the key benefits of standard form over slope-intercept or point-slope form is that it can be used to quickly find the x-intercept. It can also be used to find the y-intercept of a line, but this is something that is also relatively easy using either of the other forms. Once the x-intercept and y-intercept are known, standard form can also be used to graph the line, though it is slightly more tedious than using either of the other two mentioned forms.
Standard form is also the form of a linear equation that is typically used when solving systems of linear equations. Using either slope-intercept or point-slope form would make solving linear equations more difficult.
Linear equations are also expressed in other forms, but the above are some of the most common.
