Slope intercept form
Slope-intercept form one of a number of different forms of a linear equation. It is one of the most commonly used forms, and has the following structure:
y = mx + b
In the equation above, m is the slope, and b is the y-intercept. Slope intercept form is useful because it allows us to quickly identify the slope and y-intercept of a line, which in turn allows us to graph the line fairly easily.
Given a point and the slope of a line, you can write a linear equation in slope-intercept form.
Example
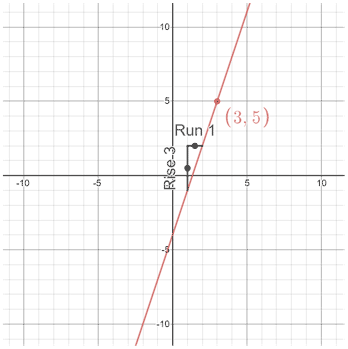
Given m = 3 and the point (3, 5), find b, and write the equation of the line in slope-intercept form.
|
|
Because we are given slope and a point on a line, we just need to find the y-intercept in order to write the equation of the line in slope-intercept form. We found the y-intercept by plugging the given values into the equation y = mx + b, then solving for b. Once the slope and y-intercept are known, writing the equation of the line just involves plugging the slope and y-intercept into m and b respectively.
How to find the slope and the y-intercept
Given at least two points on a line, the slope of the line can be found using the slope formula:
For example, given the that (1, 5) and (-2, 7) are points on the same line, the slope of the line can be found as follows:
The y-intercept can be found in a number of ways. If a graph is given, the point at which the line intersects the y-axis is the y-intercept. This occurs when x = 0. It follows that, given an equation, setting x equal to 0 and solving for y will yield the y-intercept of the line. For example, given the line 3x + 2y = 6, the y-intercept can be found by plugging 0 in for x, then solving for y.
3(0) + 2y = 6
2y = 6
y = 3
Thus, the y-intercept occurs at the point (0, 3).
Other forms of linear equations
Slope-intercept form is just one of a number of different forms of linear equations, albeit it is the most commonly used form. Depending on the context that a linear equation is being used in, certain forms can be more beneficial to use. Other commonly used forms include point-slope form and standard form.
Slope-intercept form is useful because the slope and y-intercept of the line can easily be read off the equation, which also makes it relatively easy to graph the line, since we can just start from the y-intercept and find another point on the line by counting the rise over run (slope) in the coordinate plane.
Point-slope form
Point-slope form can be generalized as:
y - y1 = m(x - x1)
In the equation, y1 and x1 indicate a point on the line that is not the y-intercept, while m is the slope. Point-slope form is useful when a point on the line and the slope of the line are known, since it enables us to write an equation for the line.
Standard form
The standard form of the equation of a line is
Ax + By = C
where A, B, and C are integers. Standard form is useful when we are trying to solve systems of linear equations. It can also be used to write the equation of vertical lines, something that cannot be done using slope-intercept or point-slope form.
Converting between different forms
It is relatively common to need to convert the equation of a line in standard or point-slope form to slope-intercept form.
Standard to slope-intercept form
Converting from standard form to slope-intercept form involves manipulating an equation in standard form so as to isolate y on one side of the equation such that the coefficient on the y is 1.
Example
Convert 2x - 5y + 6 = 0 to slope-intercept form.
5y = 2x + 6
y = 2x/5 + 6/5
The slope is therefore 2/5, and the y-intercept is at (0, 6/5).
Point-slope to slope-intercept form
Converting from point-slope form to slope-intercept form is relatively simple since both already include a slope, so all we need to do is convert the equation such that we can read off the y-intercept, rather than some other point on the line.
Example
Convert y - 7 = 1/2(x - 4) to slope-intercept form.
y = 1/2x - 4/2 + 7
y = 1/2x + 5