Rotation
In geometry, a rotation is a type of transformation where a shape or geometric figure is turned around a fixed point. It may also be referred to as a turn. A rotation is a type of rigid transformation, which means that the size and shape of the figure does not change; the figures are congruent before and after the transformation. Below are two examples.
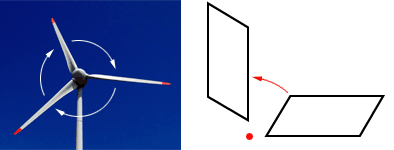
In the figure above, the wind rotates the blades of a windmill. On the right, a parallelogram rotates around the red dot.
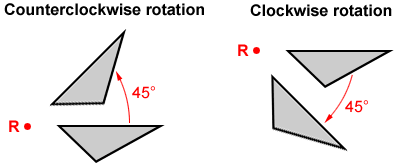
The term "preimage" is used to describe a geometric figure before it has been transformed and the term "image" is used to describe it after it has been transformed. For 2D figures, a rotation turns each point on a preimage around a fixed point, called the center of rotation, a given angle measure. Two Triangles are rotated around point R in the figure below. For 3D figures, a rotation turns each point on a figure around a line or axis.
Rotational symmetry
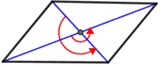
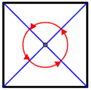
A geometric figure or shape has rotational symmetry about a fixed point if it can be rotated back onto itself by an angle of rotation of 180° or less. Below are several geometric figures that have rotational symmetry. The order of rotational symmetry is the number of times a figure can be rotated within 360° such that it looks exactly the same as the original figure.
Rotations in coordinate geometry
In a coordinate plane, when geometric figures rotate around a point, the coordinates of the points change. While a geometric figure can be rotated around any point at any angle, we will only discuss rotating a geometric figure around the origin at common angles.
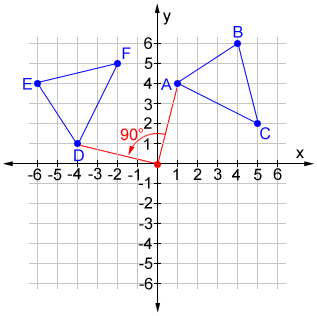
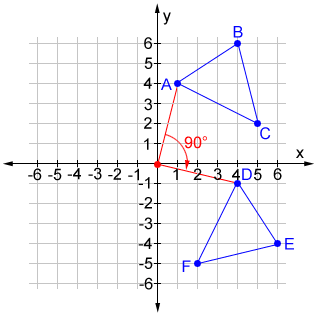
90° rotation
A rotation of 90° counterclockwise around the origin changes the position of a point (x, y) such that it becomes (-y, x). A rotation of 90° clockwise changes the point such that (x, y) becomes (y, -x).
180° rotation
A rotation of 180° (either clockwise or counterclockwise) around the origin changes the position of a point (x, y) such that it becomes (-x, -y).
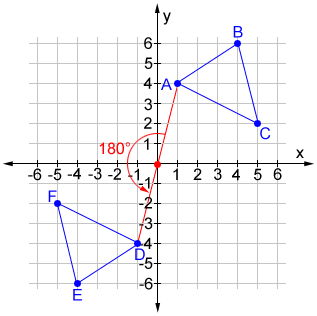
Triangle ABC has vertices A (1, 4), B (4, 6) and C (5, 2). It is rotated 180° counterclockwise to land on DEF, which has vertices D (-1, -4), E (-4, -6), and F(-5, -2). A clockwise rotation of 180° for triangle ABC also results in triangle DEF.
