Translation
In geometry, a translation is a type of a transformation that moves a geometric figure in a given direction without changing the size or orientation of the figure. It is a type of rigid transformation, which means that the figures are congruent before and after the transformation.

In the figure above, the red arrows indicate the direction of movement. Only the position of the objects changes.
The term "preimage" is used to describe a geometric figure before it has been transformed and the term "image" is used to describe it after it has been transformed.
In more exact terms, a translation moves every point on the preimage the same distance in a given direction. Rays or vectors are often used to depict a translation. Triangle ABC is translated to triangle DEF below.
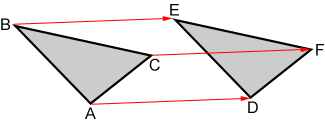
The three vectors, displayed as red rays above, show how triangle ABC is translated to DEF.
Example:
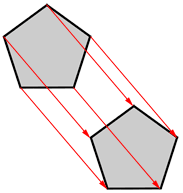
Translate the pentagon below using the given vector.
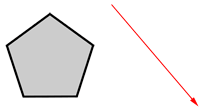
Place the tail of a vector on each of the 5 vertices of the pentagon. The head of each vector is a vertex of the translated pentagon.
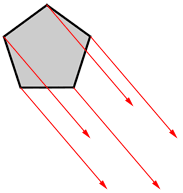
Draw line segments between the vertices of the translated pentagon.
Translations in coordinate geometry
A translation in the coordinate plane moves every point on a figure a given distance in a given direction. The position of any point (x, y) on the figure changes to (x + a, y + b), where a and b are real numbers. Rectangle ABCD is translated both vertically and horizontally to land on rectangle EFGH in the figure below.
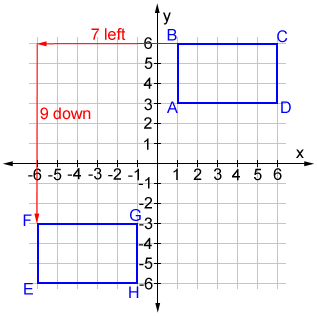
Every point of rectangle ABCD is translated 7 units left then 9 units down to form EFGH. Based on the figure above, a = -7 and b = -9. The coordinates for all the points of the translated rectangle EFGH can be found relative to the position of ABCD by using (x - 7, y - 9) for all points on ABCD.
Example:
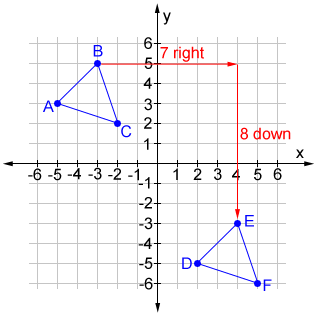
If (x, y) is a point on triangle ABC, graph the translated triangle DEF given the coordinates (x + 7, y - 8).
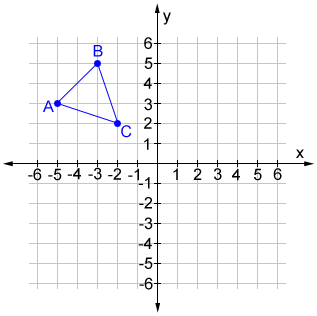
The value for a is 7 and b is -8 so, each vertex in triangle ABC is translated 7 units to the right then 8 units down to produce the vertices of triangle DEF.