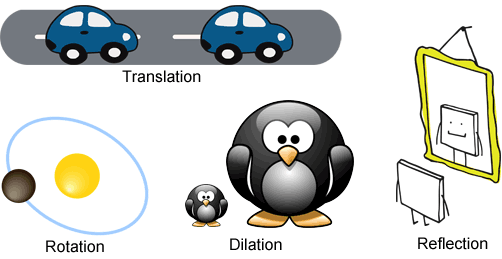
Transformation

In geometry, a transformation moves or alters a geometric figure in some way (size, position, etc.). Below are several examples.

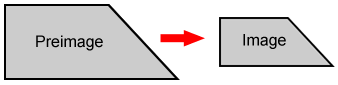
In a transformation, the original figure is called the preimage and the figure that is produced by the transformation is called the image.

Types of transformations

Below are four common transformations. Translation, reflection, and rotation are all rigid transformations, while dilation is a non-rigid transformation. Rigid transformations are transformations that preserve the shape and size of the geometric figure. Only position or orientation may change, so the preimage and image are congruent. In non-rigid transformations, the preimage and image are not congruent.

Translation

A translation moves every point on the preimage the same distance in a given direction.

Reflection

A reflection produces a mirror image of a geometric figure.

Rotation

A rotation turns each point on the preimage a given angle measure around a fixed point or axis.

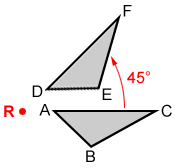
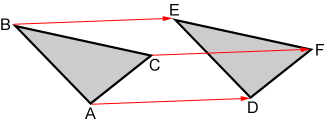
Each point on triangle ABC is rotated 45° counterclockwise around point R, the center of rotation, to form triangle DEF. A rotates to D, B rotates to E, and C rotates to F. Triangles ABC and DEF are congruent.

Dilation

A dilation increases or decreases the size of a geometric figure while keeping the relative proportions of the figure the same.

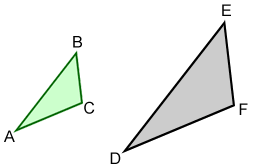
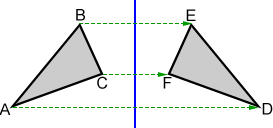
In the above figure, triangle ABC or DEF can be dilated to form the other triangle. The triangles are not congruent, but are similar. Each of the corresponding sides is proportional, so either triangle can be used to form the other by multiplying them by an appropriate scale factor. The scale factor that would be used to form DEF from ABC is the reciprocal of the scale factor that would be used to form ABC from DEF. Assuming that ABC is twice the size of DEF, the scale factor to form ABC from DEF would be 0.5. To form DEF from ABC, the scale factor would be 2.