Reflection
A reflection is a type of geometric transformation in which a shape is flipped over a line.
Reflection definition
In geometry, a reflection is a rigid transformation in which an object is mirrored across a line or plane. When an object is reflected across a line (or plane) of reflection, the size and shape of the object does not change, only its configuration; the objects are therefore congruent before and after the transformation. The figure below shows several examples:

The term "preimage" is used to describe a geometric figure before it has been transformed; "image" is used to describe it after it has been transformed.
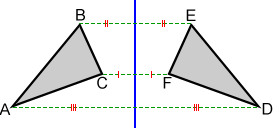
In a reflection of a 2D object, each point on the preimage moves the same distance across the line of reflection to form a mirror image of itself. The same is true for a 3D object across a plane of refection. The figure below shows the reflection of triangle ABC across the line of reflection (vertical line shown in blue) to form triangle DEF. A, B, and C are the same distance from the line of reflection as their corresponding points, D, E, and F. This is true for any corresponding points on the two triangles and this same concept applies to all 2D shapes.
Reflections in the coordinate plane
There are a number of different types of reflections in the coordinate plane. The most common cases use the x-axis, y-axis, and the line y = x as the line of reflection.
Reflection over x axis
In a reflection about the x-axis, the x-coordinates stay the same while the y-coordinates take on their opposite signs. Algebraically, the ordered pair (x, y) becomes (x , -y).
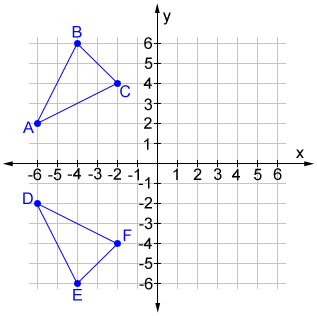
Triangle ABC has vertices A (-6, 2), B (-4, 6), and C (-2, 4). Triangle DEF is formed by reflecting ABC across the x-axis and has vertices D (-6, -2), E (-4, -6) and F (-2, -4). All of the points on triangle ABC undergo the same change to form DEF.
Reflection over y axis
In a reflection about the y-axis, the y-coordinates stay the same while the x-coordinates take on their opposite sign. Algebraically, the ordered pair (x, y) becomes (-x, y).

Triangle ABC has vertices A (-4, -6), B (-6, -2), and C (-2, -4). Triangle DEF is formed by reflecting ABC across the y-axis and has vertices D (4, -6), E (6, -2) and F (2, -4). All of the points on triangle ABC undergo the same change to form DEF.
Reflection over y = x
A reflection across the line y = x switches the x and y-coordinates of all the points in a figure such that (x, y) becomes (y, x).
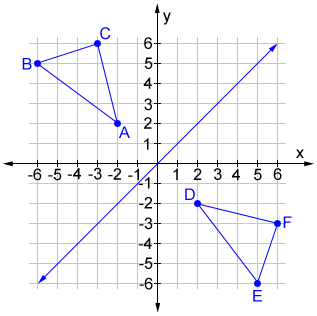
Triangle ABC is reflected across the line y = x to form triangle DEF. Triangle ABC has vertices A (-2, 2), B (-6, 5) and C (-3, 6). Triangle DEF has vertices D (2, -2), E (5, -6), and F (6, -3). All of the points on triangle ABC undergo the same change to form DEF.
Reflection over a horizontal or vertical line
To reflect objects over horizontal or vertical lines that are not the x- or y-axes, the following steps can be used:
- Draw the line of reflection.
- Consider the line of reflection and object being reflected to be a single object.
- Translate the line and object such that a horizontal line is mapped to the x-axis, or a vertical line is mapped to the y-axis. For example, given the vertical line y = -2, translating the line (as well as the object) 2 units to the right would map the line to the y-axis.
- Perform the reflection as we would in the x-axis or y-axis reflection examples above.
- Undo the translation that mapped the horizontal or vertical line to the corresponding axis. Referencing the example in step 3, we would shift the reflected object 2 units to the left after reflecting it.
This is just one way to reflect objects over a horizontal or vertical line. It is possible to mostly perform the reflection by sight with the understanding that the reflected object will lie an equal distance from the line of reflection as the original.
Reflection over the origin
Objects can also be reflected over any point in the coordinate plane. The simplest and most commonly used point is the origin. Reflection about the origin can be thought of as reflecting across the x-axis and then the y-axis (or vice versa). This essentially means changing the sign of every x- and y-value to its opposite sign. In other words, the ordered pair (x, y) becomes (-x, -y).
Although the base concept remains the same for any point, in practice, if the point of reflection is not the origin, we cannot simply change the sign of the x- and y-coordinates to find the coordinates of the reflection. We can however use a similar strategy as described above for reflections over a horizontal or vertical line. To find a reflection about a point,
- Find the coordinates of the point of reflection.
- Translate the point of reflection as well as the object such that the point of reflection is mapped to the origin. For example, given the point of reflection (-1, 3), move the point (as well as the object) 1 unit to the right and 3 units down.
- Perform a reflection about the origin by changing the sign of all the x- and y-coordinates of the translated object to the opposite sign.
- Undo the translation performed in step 2, shifting the preimage and point of reflection back to their original positions, along with the new image.
- The final position of the image is the reflection of the object about the given point.
Note that in all of the examples above, the shapes we reflected lie entirely on one side of the line or point of reflection. If parts of the object cross the line of reflection, treat the parts of the object on different sides separately. For example, given an object that crosses the y-axis, we can reflect the object by reflecting the left side over the y-axis first, then reflecting the part on the right again across the y-axis. This same logic can be used for the other types of reflections described above.
Reflection symmetry
A line of reflection is also a line of symmetry if a geometric shape or figure can be reflected across the line back onto itself.

Reflecting the right side of the butterfly across line l maps it to the butterfly's left side. The same result occurs if the left side of the butterfly is reflected across line l, so line l is also a line of symmetry. You can think of folding half of the image of the butterfly across the line of reflection back on to its other half.
Whenever you reflect a figure across a line of reflection that is also a line of symmetry, each point on the figure is translated an equal distance across the line of symmetry, back on to the figure.
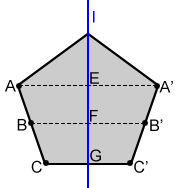
Let line l be a line of reflection for the pentagon above. Points A, B, and C on the pentagon are reflected across line l to A', B', and C'. AE = A'E, BF = B'F, and CG = C'G. This is true for the distances between any corresponding points and the line of reflection, so line l is also a line of symmetry.
Reflection symmetry and even and odd functions
One of the applications of reflections arises in algebra, where functions can either be even or odd.
- A function is even if it is symmetric about the y-axis. In other words, imagine folding the graph of the function over the y-axis; if it folds on top of itself, the function is even.
- A function is odd if it has symmetry about the origin. In other words, if flipping the graph of the function about the x-axis and then y-axis (or vice versa) results in the graph folding onto itself, the function is odd.
Glide reflection
A glide reflection is a combination (also referred to as a composition) of a translation followed by a reflection.
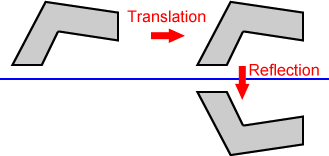
The preimage of a concave hexagon is translated to the right then reflected across the line of reflection to produce the final image shown above.
