Scale factor
A scale factor is the ratio between the size of an original and final object that vary only in size. For example, the penguin shown on the left below is 3 times larger than the penguin on the right. The factor we would scale the larger penguin by to get the smaller penguin is the scale factor. In this case, the scale factor is ⅓. Similarly, the pentagon shown in green is enlarged by a scale factor of 2 to produce the blue pentagon.
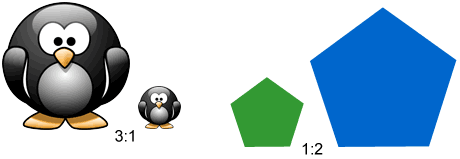
What is a scale factor
A scale factor is the ratio between corresponding measurements of two similar figures. In geometry, a similar figure is one that has the same shape and angle measurements but a different size; a corresponding side is one that is in the same relative position of the different figures. The scale factor is the factor by which the dimensions of one figure need to be multiplied by in order to make the other figure. There are a few different ways for an object can be scaled:
- Enlargement: When an object becomes larger as a result of the scale factor, this is referred to as enlargement. When an object is enlarged, the scale factor is always > 1.
- Reduction: When an object becomes smaller as a result of the scale factor, this is referred to as reduction. When an object is reduced, the scale factor is always < 1.
- Congruent: When an object stays the same size as a result of the scale factor, the objects are congruent, and the scale factor is = 1.
Scale factor formula
The formula for finding the scale factor is:
For example, if the original shape is a square with side lengths of 4 and the final shape is a square with side lengths of 6, the scale factor is:
This means that we multiply all sides of the original square by 3/2 to get the final square.
Recall that when an object is scaled, only the dimensions change. The angle measures stay the same. Also, all dimensions of the object must be scaled by the same scale factor. If we compare two objects and find a different scale factor, this means that the two objects are not similar, and there is no scale factor.
How to use scale factor
There are a number of practical uses for scale factors:
- Drawing similar figures in geometry.
- Making scale models, such as train models that fit in a living room but have the same proportions as the real thing.
- Creating blueprints for large machinery or structures, which allows us to visualize large real-world objects in small spaces.
- Making maps that accurately represent real-world distances.
- Providing a reference scale on graphs that can clarify or simplify data presentation.
Scaling geometric figures
The scale factor tells us what to multiply each side length of a geometric figure by to produce a scaled, similar figure.
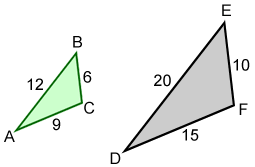
Triangle ABC is similar to triangle DEF (△ABC~△DEF), which means that the corresponding side lengths of the triangles are proportional:
Any of the three ratios can be used to determine the scale factor.
Example:
Find the lengths of sides b and d for the triangles below given that △ABC~△DEF.
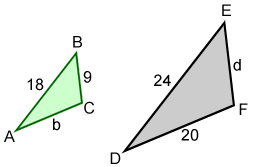
Since the triangles are similar, . We can find the scale factor using the ratio of a pair of corresponding sides:
. This is the scale factor we multiply a side length of triangle ABC by to find its corresponding side length in DEF. We would multiply a side length of DEF by
instead to find its corresponding side length in ABC.
We could also set the ratios of the corresponding sides equal to find b and d.
|
18d = 216 d = 12 |
24b = 360 b = 15 |
