y intercept
The y-intercept of a function is the point at which the graph of the function crosses the y-axis. Although a function can have many x-intercepts, a function can only have one y-intercept. This is because a function must pass the vertical line test in order for it to be a function; if a vertical line intersects the graph of a relation at more than one point, it is not a function.
Example
The relation in the following figure is a function because it passes the vertical line test.

The relation in the following figure is not a function because it fails the vertical line test. It has more than one y-intercept and many points at which a vertical line would cross the graph more than once.

How to find the y-intercept of a function
To find the y-intercept of a function, we need to find the point on the graph where x = 0. Given a function, f(x), the y-intercept occurs at f(0).
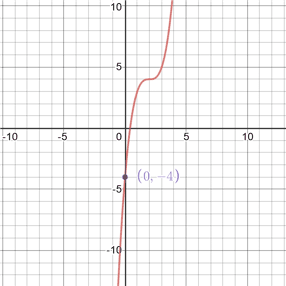
Example
Find the y-intercept of: f(x) = (x - 2)3 + 4
f(0) = (0 - 2)3 + 4
f(0) = -8 + 4 = -4
Thus, the y-intercept is at (0, -4).