Similar figures
In Geometry, two or more figures or objects are similar if they have the same shape but not necessarily the same size. For polygons, corresponding angles have the same measure, and corresponding sides are proportional. All circles are similar circles. Below are three sets of similar geometric figures.
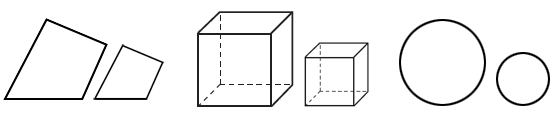
We see similarity all around us. Below on the left are similar leafs. The pyramids of Egypt on the right are similar pyramids.

Properties of similarity
Two geometric figures are similar if they have the same shape but not necessarily the same size and have the following properties:
- Corresponding angles are congruent
- Corresponding sides are proportional
The mathematical symbol "~" is used to indicate similar geometric figures.
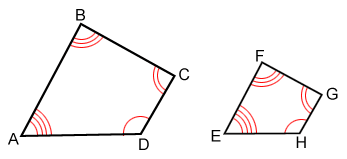
The two quadrilaterals above have the following angle and side length relationships:
Angles: ∠A≅∠E, ∠B≅∠F, ∠C≅∠G, and ∠D≅∠H
Sides:
Therefore, quadrilateral ABCD ~ EFGH.
Producing similar figures
The dilation transformation produces similar figures that are not necessarily the same size.
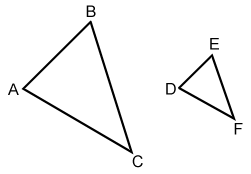
△ABC is dilated by a factor of (its size is reduced by
but its shape is the same) to produce △DEF so that
,
, and
. The ratios of the sides are:
,
, and
, and the shape of the triangles is the same. Therefore, ∠A≅∠D, ∠B≅∠E, ∠C≅∠F and we can conclude that △ABC~△DEF.
Translations, reflections, and rotations produce congruent figures that are also similar. The corresponding angles are congruent and the ratios of the corresponding sides equal 1. (See the article for Congruent to learn more about these transformations and congruency).
Proving similarity in polygons
Any two polygons are similar if their corresponding angles are congruent and the ratios of their corresponding sides are equal.
Of the many different shapes in geometry, similar triangles are used most frequently. Refer to the similar triangles page to see methods for determining the similarity of triangles.
