Arcsin
Arcsine, written as arcsin or sin-1 (not to be confused with ), is the inverse sine function.
Arcsin graph
The graph of y = arcsin(x) is shown below:
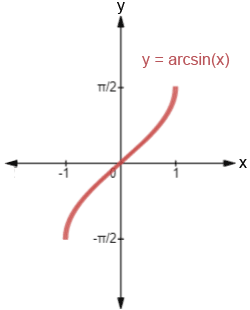
The domain of y = arcsin(x) is and its range is
. One of the properties of inverse functions is that if a point (a, b) is on the graph of f, the point (b, a) is on the graph of its inverse. This effectively means that the graph of the inverse function is a reflection of the graph of the function across the line y = x. We can see this if we look at the graph of y = sin(x) below:
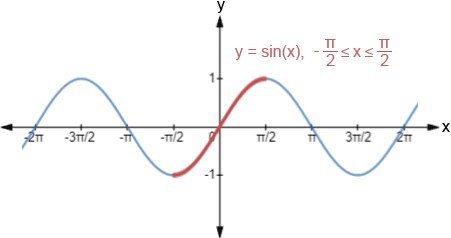
Notice that sine only has an inverse on a restricted domain, , highlighted in red, and that this restricted domain is the range of y = arcsin(x). The reason that the domain of y = sin(x) must be restricted is because in order for a function to have an inverse, the function must be one-to-one, which means that no horizontal line can intersect the graph of the function more than once. Since sine is a periodic function, without restricting the domain, a horizontal line would intersect the function periodically, infinitely many times.
Arcsine calculator
The following is a calculator to find out either the arccos value of a number between -1 and 1 or cosine value of an angle.
Using special angles to find arcsin
While we can find the value of arcsine for any x value in the interval [-1, 1], there are certain angles that are used frequently in trigonometry (0°, 30°, 45°, 60°, 90°, and their multiples and radian equivalents) whose sine and arcsine values may be worth memorizing. Below is a table showing these angles (θ) in both radians and degrees, and their respective sine values, sin(θ).
| θ | -90° | -60° | -45° | -30° | 0° | 30° | 45° | 60° | 90° |
| sin(θ) | -1 | 0 | 1 |
One method that may help with memorizing these values is to express all the values of sin(θ) as fractions involving a square root. Starting from 0° progressing through 90°, sin(0°) = 0 = . The subsequent values, sin(30°), sin(45°), sin(60°), and sin(90°) follow a pattern such that using the value of sin(0°) as a reference, to find the values of sine for the subsequent angles, we simply increase the number under the radical sign in the numerator by 1, as shown below.
| θ | 0° | 30° | 45° | 60° | 90° |
| sin(θ) |
The values of sine from 0° through -90° follows the same pattern except that the values are negative instead of positive since sine is negative in quadrant IV. This pattern repeats periodically for the respective angle measurements, and we can identify the values of sin(θ) based on the position of θ in the unit circle, taking the sign of sine into consideration: sine is positive in quadrants I and II and negative in quadrants III and IV.
Once we've memorized the values, or if we have a reference of some sort, it becomes relatively simple to recognize and determine sine or arcsine values for the special angles.
Example:
Find arcsin(), arcsin(
), and arcsin(3) in radians.
,
.
,
.
arcsin(3) is undefined because 3 is not within the interval -1≤arcsin(θ)≤1, the domain of arcsin(x).
Inverse properties
Generally, functions and their inverses exhibit the relationship
f(f-1(x)) = x and f-1(f(x)) = x
given that x is in the domain of the function. The same is true of sin(x) and arcsin(x) within their respective restricted domains:
sin(arcsin(x)) = x, for all x in [-1, 1]
and
arcsin(sin(x)) = x, for all x in [,
]
These properties allow us to evaluate the composition of trigonometric functions.
Composition of arcsine and sine
If x is within the domain, evaluating a composition of arcsine and sine is relatively simple.
Examples:
1.
2.
If x is not within the domain, we need to determine the reference angle as well as the relevant quadrant. Given arcsin(sin() ), we cannot evaluate this as we did above because x is not within [
,
], so the solution cannot be
. To evaluate this, we first need to determine sin(
) before using arcsin:
3.
In the above example, the reference angle is and sin(
) is
. However,
is in quadrant III where sin is negative, so sin(
) =
, and the only angle within the domain of arcsin(x) whose sine is
is
.
Composition of other trigonometric functions
We can also make compositions using all the other trigonometric functions: cosine, tangent, cosecant, secant, and cotangent.
Example:
Find cos(arcsin()).
Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Given arcsin(
)=θ, we can find that sin(θ)=
. The right triangle below shows θ and the ratio of its opposite side to the triangle's hypotenuse.
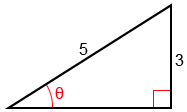
To find cosine, we need to find the adjacent side since cos(θ)=. Let b be the length of the adjacent side. Using the Pythagorean Theorem,
32 + b2 = 52
9 + b2 = 25
b2 = 16
b = 4
We know that arcsin() = θ, so we can rewrite the problem and find cos(θ) by using the triangle we constructed above and the fact that cos(θ)=
:
cos(arcsin()) = cos(θ) =
The same process can be used with a variable expression.
Example:
Find tan(arcsin(2x)).
Given arcsin(2x) = θ, we can find that sin(θ) = and construct the following triangle:
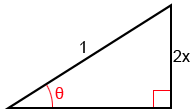
To find tangent, we need to find the adjacent side since tan(θ)=. Let b be the length of the adjacent side. Using the Pythagorean theorem,
(2x)2 + b2 = 12
4x2 + b2 = 1
b2 = 1 - 4x2
b =
and
tan(arcsin(2x)) = tan(θ) = , where
<x<
Using arcsine to solve trigonometric equations
Arcsine can also be used to solve trigonometric equations involving the sine function.
Examples:
Solve the following trigonometric equations for x where 0≤x<2π.
1. 2sin(x) =
2sin(x) =
sin(x) =
Sine is positive in two quadrants, quadrant I and quadrant II, so there are two solutions: x= and x=
. These are the only two angles within 0≤x<2π whose sine value is equal to
.
2. 2sin2(x) + 5sin(x) - 3 = 0
2sin2(x) + 5sin(x) - 3 = 0
(2sin(x) - 1)(sin(x) + 3) = 0
2sin(x) - 1 = 0 or sin(x) + 3 = 0
sin(x) = or sin (x) = -3
x = arcsin() or x = arcsin(-3)
Solving for x = arcsin(),
x= or
We cannot solve for x = arcsin(-3) because it is undefined, so x= or
are the only solutions.
