Trigonometry

Trigonometry (named based on a Greek word that loosely translates to "measurement of triangles") is a branch of mathematics that studies the relationships between the sides and angles of triangles. Trigonometry has many practical applications and is used in astronomy, surveying, navigation, and more.

Trigonometric functions

The relationships between the sides and angles of triangles are related with trigonometric functions. There are two main ways in which trigonometric functions are typically discussed: in terms of right triangles and in terms of the unit circle. The right-angled triangle definition of trigonometric functions as described below is most often how they are introduced.

Right triangle definition

The output of a trigonometric function is a ratio of the lengths of two sides of a right triangle. The terms used to describe the sides of a right triangle are the hypotenuse, the adjacent side, and the opposite side, as shown in the figure below.

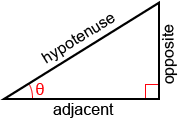
The sides of a right triangle are referenced as follows:

The trigonometric functions are defined based on the ratios of two sides of the right triangle. There are six trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. These functions are often abbreviated as sin, cos, tan, csc, sec, and cot. Their definitions are shown below.

sine:
cosine:
tangent:
cosecant:
secant:
cotangent:

Sine, cosine, and tangent are the three most commonly used trigonometric functions. Cosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent, respectively. As such, as long as we remember the definitions of sine, cosine, and tangent, we can take their reciprocals to determine the definitions of cosecant, secant, and cotangent.

Example:

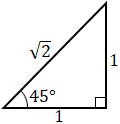
What is the value of sin(45°), cos(45°), and tan(45°)?

Example:

Bob walked 300 m straight up on a 30° hill, how high did Bob climb?

Height = distance walked × sin(30°)
= 300 × 0.5
= 150 m

Thus, Bob reached a height of 150 m after walking 300 m up the slope of the hill.

Trigonometric identities

Trigonometric identities are equations that are used to describe the many relationships that exist between the trigonometric functions. Among other uses, they can be helpful for simplifying trigonometric expressions and equations.

The below shows some of the identities you may encounter in your study of trigonometry.

Reciprocal identities

sin(θ)·csc(θ) = 1
cos(θ)·sec(θ) = 1
tan(θ)·cot(θ) = 1

Quotient identities

Cofunction identities

Odd/even identities

sin(-θ) = -sin(θ)
cos(-θ) = cos(θ)
tan(-θ) = -tan(θ)
csc(-θ) = -csc(θ)
sec(-θ) = sec(θ)
cot(-θ) = -cot(θ)

Pythagorean identities

cos2(θ) + sin2(θ) = 1
1 + tan2(θ) = sec2(θ)
1 + cot2(θ) = csc2(θ)

Example:

Simplify the following

=
=
=
=
=

Trigonometric formulas

There are many formulas used in trigonometry that involve one or more angles or sides of a triangle.

Sum and difference formulas

sin(x ± y) = sin(x)·cos(y) ± cos(x)·sin(y)
cos(x ± y) = cos(x)·cos(y) ∓ sin(x)·sin(y)

Double angle formulas

sin(2θ) = 2·sin(θ)·cos(θ)
cos(2θ) = cos2(θ) - sin2(θ) = 1 - 2·sin2(θ) = 2·cos2(θ) - 1

Half angle formulas

Non-right triangles

The right triangle definitions of trigonometric functions only apply to right triangles. They cannot be used for non-right triangles, such as triangle ABC below, which is an oblique triangle.

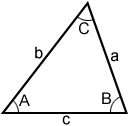
Rather, the following triangle identities can be used to relate the sides and angles of triangle ABC.

The sine rule

The Law of Sines can be used when one side and any two angles are given for an oblique triangle, or when one angle and two sides are given.

Example:

For triangle ABC, a=3, B=70°, C=45°, find A, b, and c,

A = 180° - B - C = 180° - 70° - 45° = 65°

The cosine rule

a2 = b2 + c2 - 2bc·cos(A)
b2 = a2 + c2 - 2ac·cos(B)
c2 = a2 + b2 - 2ab·cos(C)

The Law of Cosines can be used when one angle and its two included sides are given for an oblique triangle, or when all three sides are given.

Example:

For triangle ABC, A=45°, b=3, c=5, find a,

a2= b2 + c2 - 2bc·cos(A)
 = 32 + 52 - 2×3×5×cos(45°)
 = 12.787