Trigonometric functions
Trigonometric functions are functions related to an angle. There are six trigonometric functions: sine, cosine, tangent and their reciprocals cosecant, secant, and cotangent, respectively. Sine, cosine, and tangent are the most widely used trigonometric functions. Their reciprocals, though used, are less common in modern mathematics. Trigonometric functions are also called circular functions.
6 trig functions
The table below shows the six trigonometric function values for the specified angles in both degrees and radians.
| θ | 0° / 0 | 30° / |
45° / |
60° / |
90° / |
180° / |
270° / |
360° / |
|---|---|---|---|---|---|---|---|---|
| sin(θ) | 0 | 1 | 0 | -1 | 0 | |||
| cos(θ) | 1 | 0 | -1 | 0 | 1 | |||
| tan(θ) | 0 | 1 | Undefined | 0 | Undefined | 0 | ||
| csc(θ) | Undefined | 2 | 1 | Undefined | -1 | Undefined | ||
| sec(θ) | 1 | 2 | Undefined | -1 | Undefined | 1 | ||
| cot(θ) | Undefined | 1 | 0 | Undefined | 0 | Undefined |
Although the table does not include the multiples of each angle in each quadrant, we can use the table to find the values of the other angles; the values are the same for each corresponding angle, taking the sign of the respective quadrant into consideration. For example, the value of cosine for 30° or in the first quadrant is
. Since the values of cosine in quadrants II and III are negative, the value for cosine for the corresponding angles in quadrants II and III (150° and 210°) is
. Similarly, since the value for cos(330°) in quadrant IV is positive, it has the same value as cos(30°). We can find the values of the other trigonometric functions in the same way. Refer to the reference angles section below for more detail as well as a table of the signs of the six trigonometric functions in each quadrant.
Trigonometric function definitions
There are two main ways in which trigonometric functions are typically discussed: in terms of right triangles and in terms of the unit circle. The right-angled triangle definition of trigonometric functions is most often how they are introduced, followed by their definitions in terms of the unit circle.
Right triangle definition
The output of a trigonometric function is a ratio of the lengths of two sides of a right triangle. Consider an angle θ as one angle in a right triangle. The following are the definitions of the trigonometric functions. These functions are often written in their abbreviated forms.
| sine: | |
| cosine: | |
| tangent: |
| cosecant: | |
| secant: | |
| cotangent: |
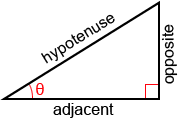
The terms used to describe the sides of a right triangle are the hypotenuse, the adjacent side, and the opposite side, as shown in the figure above.
- Adjacent: the side next to θ that is not the hypotenuse
- Opposite: the side opposite θ.
- Hypotenuse: the longest side of the triangle opposite the right angle.
A common method for remembering the above relationships is through use of the mnemonic “soh cah toa.” The s, c, and t stand for sine, cosine, and tangent, and o, a, and h stand for opposite, adjacent, and hypotenuse.
Cosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent, respectively. As such, as long as we remember the definitions of sine, cosine, and tangent, we can take their reciprocals to determine the definitions of cosecant, secant, and cotangent.
Example:
Find the values of the six trigonometric given the right triangle below.
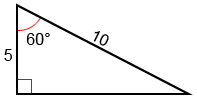
The hypotenuse of the triangle is 10, and the adjacent side has a length of 5. Using the Pythagorean theorem, we can find the length of the third, opposite, side:
52 + b2 = 102
25 + b2 = 100
b2 = 75
Now that we know all the sides of the triangle with reference to the angle, 60°, we can plug them into the trigonometric functions as defined above:
Unit circle definition
Trigonometric functions can also be defined as coordinate values on a unit circle. A unit circle is a circle of radius 1 centered at the origin. The right triangle definition of trigonometric functions allows for angles between 0° and 90° (0 and in radians). Using the unit circle definitions allows us to extend the domain of trigonometric functions to all real numbers. Refer to the figure below.
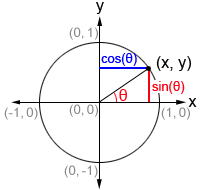
Given a point (x, y) on the unit circle, we can form a right triangle, as shown in the figure. In such a triangle, the hypotenuse is the radius of the unit circle, or 1. θ is the angle formed between the initial side of an angle along the x-axis and the terminal side of the angle formed by rotating the ray either clockwise or counterclockwise. The terminal side of the angle is the hypotenuse of the right triangle and is the radius of the unit circle. Therefore, it always has a length of 1. The point at which the terminal side of the angle intersects the unit circle has an x-value of cos(θ) and y-value of sin(θ).
Thus, on the unit circle, cosine and sine can be defined as:
For tan(θ), x cannot be equal to 0.
Cosecant, secant, and cotangent are the reciprocals of sine, cosine, and tangent respectively, and are defined as:
The values of the trigonometric functions can also be represented by the lengths of the line segments in a coordinate plane with a unit circle as show in the diagram below.
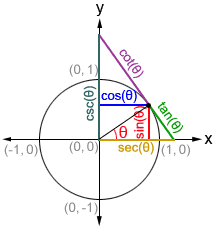
Trigonometric function values for the special angles
The values of trigonometric functions can be found through the coordinate values of the intersections on a unit circle. While we can find the value of any of the trigonometric functions for any value of θ, there are some angles that are more frequently used in trigonometry and worth memorizing.
Reference angles
Acute angles in the first quadrant can be used to determine the values of trigonometric functions of angles in other quadrants. Below is a table of the values of the sine, cosine, and tangent functions for special angles in the first quadrant, referred to as reference angles.

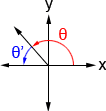
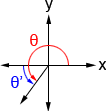
These angles are called reference angles since we will reference their values to determine other values. It is always the smallest angle (with reference to the x-axis) that can be made from the terminal side of an angle. The figures below shows an angle θ and its reference angle θ' in a quadrant other than the first quadrant.
| Quadrant II | Quadrant III | Quadrant IV |
|---|---|---|
 |
 |
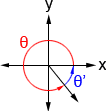 |
| θ'= 180° - θ | θ'= θ - 180° | θ'= 360° - θ |
If one angle is an reference angle of another, the trigonometric functions of these two angles have the same values in magnitude, and we just need to pay attention to their signs based on the quadrant that the terminal side of the angle lies in. For example, 30° is the reference angle of 210° with sine values sin(30°)= and sin(210°)=
. We can see that the sine values of both have a magnitude of
, albeit they have different signs.
Below is a table showing the signs of the 6 trigonometric functions in each quadrant.
| Sin | Cos | Tan | Csc | Sec | Cot | |
| Quadrant I | + | + | + | + | + | + |
| Quadrant II | + | - | - | + | - | - |
| Quadrant III | - | - | + | - | - | + |
| Quadrant IV | - | + | - | - | + | - |
Once we determine the reference angle, we can determine the value of the trigonometric functions in any of the other quadrants by applying the appropriate sign to their value for the reference angle.
Example:
Use reference angles to find the values of cos(150°) and sin(315°).
Since 150° is in quadrant II, the reference angle for 150° is, 180°-150°=30° where, cos(30°)=. Also because 150° is in quadrant II, cosine is negative then, cos(150°)=
.
Since 315° is in quadrant IV, the reference angle for 315° is, 360°-315°=45° where, sin(45)°=. Also because 315° is in quadrant IV, sine is negative then, sin(315°)=
.
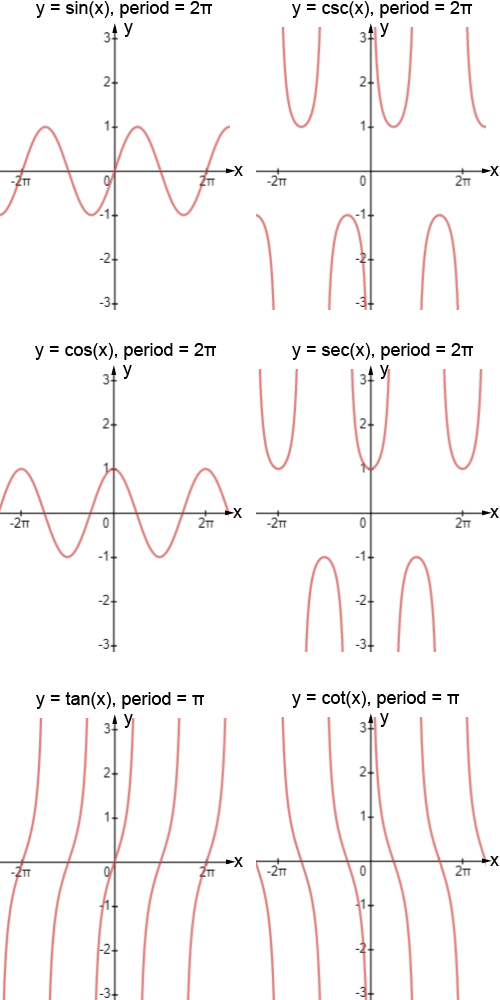
Trigonometric functions are periodic functions
A periodic function is a function, f, in which some positive value, p, exists such that
f(x+p) = f(x)
for all x in the domain of f, p is the smallest positive number for which f is periodic, and is referred to as the period of f.
All 6 trigonometric functions are periodic functions. No matter what point we start at on the unit circle, if we travel a distance of 2π (360°) along the unit circle from that point, we will arrive back at our starting point, which indicates that the trigonometric function have the same value at the angle. This means the trigonometric functions repeat their values.
The sine, cosine, cosecant, and secant functions have a period of 2π. The tangent and cotangent functions have a period of π.
sin(θ+2π) = sin (θ)
cos(θ+2π) = cos (θ)
csc(θ+2π) = csc (θ)
sec(θ+2π) = sec (θ)
tan(θ+π) = tan (θ)
cot(θ+π) = cot (θ)
Example:
Find and
using their periods.
Trigonometric functions are odd or even
An odd function is a function in which -f(x)=f(-x). It has symmetry about the origin. An even function is a function in which f(x)=f(-x) meaning that reflecting the graph across the y-axis will yield the same graph. Of the 6 trigonometric functions, sine, tangent, cosecant, and cotangent are odd functions. Cosine and secant are even functions. Therefore:
| Even functions | Odd functions |
|---|---|
|
cos(-θ) = cos(θ) sec(-θ) = sec(θ) |
sin(-θ) = -sin(θ) tan(-θ) = -tan(θ) csc(-θ) = -csc(θ) cot(-θ) = -cot(θ) |
Inverse trigonometric functions
The inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are arcsine, arccosine, arctangent, arccosecant, arcsecant, and arctangent. The input of the inverse trigonometric functions is an angle's trigonometric ratios, and its output is the angle:
|
θ = arcsin(x), where –1≤x≤1
θ = arccos(x), where –1≤x≤1
θ = arctan(x)
θ = arccsc(x), where x≤-1 or 1≤x
θ = arcsec(x), where x≤-1 or 1≤x
θ = arctan(x)
|
The inverse trigonometric functions are also written as sin-1(x), cos-1(x), tan-1(x), csc-1(x), sec-1(x), and cot-1(x).
Example:
Given sin(30°) = 0.5, what is arcsin(0.5)?
arcsin(0.5) = 30°
Note: this only provides the result in the first quadrant. If consider other quadrants, arcsin(0.5) is also equal to 150°. Also, since arcsin is a periodic function, to account for all the possible values of arcsine, we need to account for its periodicity. The solution is therefore
30°+n×360° or 150°+n×360°
where n is an integer. When using the other inverse trigonometric functions, their periodicity also needs to be taken into account to determine all the solutions.
Graphs of the trigonometric functions
The figure below shows the graphs of several periods of the six trigonometric functions. Refer to the sine, cosine, and tangent pages for an in-depth explanation on how to graph trigonometric functions that have undergone certain transformations (the same explanations apply to cosecant, secant, and cotangent, with minor differences).