Law of Sines
In trigonometry, the Law of Sines relates the sides and angles of triangles. Given the triangle below, where A, B, and C are the angle measures of the triangle, and a, b, and c are its sides, the Law of Sines states:
Generally, the format on the left is used to find an unknown side, while the format on the right is used to find an unknown angle.
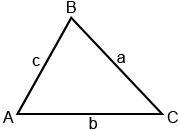
The right triangle definition of sine () can only be used with right triangles. It cannot be used to relate the sides and angles of oblique (non-right) triangles. However, there are many other relationships we can use when working with oblique triangles. The Law of Sines is one such relationship. Another is the Law of Cosines.
When to use the Law of Sines
The Law of Sines can be used to solve for the sides and angles of an oblique triangle when the following measurements are known:
- Two angles and one side: AAS (angle-angle-side) or ASA (angle-side-angle)
- Two sides and a non-included angle: SSA (side-side-angle)
Example:
For triangle ABC, a = 3, A = 70°, and C = 45°. Find B, b, and c.

We know two angles and a side (AAS) so we can use the Law of Sines to solve for the other measurements as follows:
B = 180° - (70°+45°) = 65°
When two sides and a non-included angle (SSA, the angle is not between the known sides) are known for a triangle, it is possible to construct two triangles.
Example:
Show that there are two triangles that can be formed if a = 12, c = 27, and A = 25°.
Using the Law of Sines to find angle C,
Two values of C that is less than 180° can ensure sin(C)=0.9509, which are C≈72° or 108°. The following are how the two triangles look like.
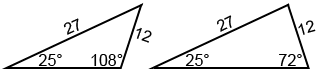
Proof of the Law of Sines
To show how the Law of Sines works, draw altitude h from angle B to side b, as shown below.
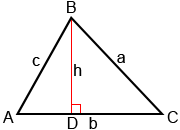
Altitude h divides triangle ABC into right triangles ADB and CDB. We can then use the right-triangle definition of sine, , to determine measures for triangles ADB and CDB.
Triangle ADB:
Triangle CDB:
Setting these two values of h equal to each other:
a·sin(C) = c·sin(A)
Next, draw altitude h from angle A instead of B, as shown below.
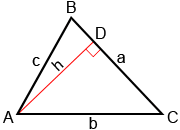
For the newly formed triangles ADB and CDB,
Triangle ADB:
Triangle CDB:
Setting these two values of h equal to each other:
b·sin(C) = c·sin(B)
Using the transitive property, we can put these two sets of equations together to get the Law of Sines:
and
